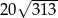Zadanie nr 9245275
Dany jest ostrosłup prawidłowy czworokątny 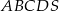 o podstawie
o podstawie 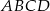 . Pole trójkąta
. Pole trójkąta 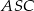 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 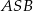 jest równy
jest równy 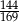 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
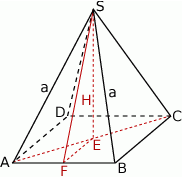
Oznaczmy przez  długość krawędzi bocznej, a przez
długość krawędzi bocznej, a przez 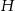 wysokość ostrosłupa. Stosując twierdzenie cosinusów w trójkącie
wysokość ostrosłupa. Stosując twierdzenie cosinusów w trójkącie 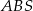 możemy obliczyć długość krawędzi podstawy.
możemy obliczyć długość krawędzi podstawy.
Zamiast stosować twierdzenie cosinusów mogliśmy obliczyć 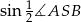 i skorzystać z definicji sinusa w trójkącie
i skorzystać z definicji sinusa w trójkącie 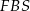 . Otrzymalibyśmy w ten sposób tę samą zależność.
. Otrzymalibyśmy w ten sposób tę samą zależność.
W takim razie
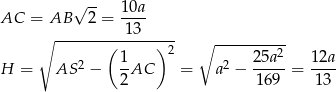
Teraz korzystamy z podanego pola trójkąta 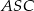 .
.
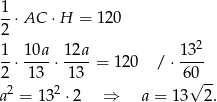
Stąd
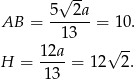
Aby obliczyć pole powierzchni bocznej obliczamy wysokość ściany bocznej – patrzymy na trójkąt prostokątny 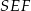 .
.
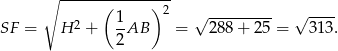
Pole powierzchni bocznej jest więc równe
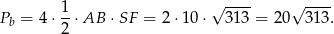
Odpowiedź: