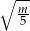Zadanie nr 7491554
W trójkącie prostokątnym 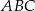 o kącie prostym w wierzchołku
o kącie prostym w wierzchołku 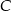 obrano taki punkt
obrano taki punkt 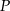 , że pola trójkątów
, że pola trójkątów 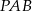 ,
, 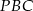 i
i 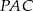 są równe. Oblicz długość odcinka
są równe. Oblicz długość odcinka 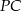 , wiedząc, że
, wiedząc, że 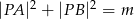 .
.
Rozwiązanie
Oczywiście najważniejszy jest rysunek.
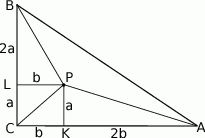
Ponieważ trójkąty 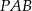 ,
, 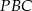 i
i 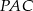 mają równe pola, to pole każdego z nich to dokładnie
mają równe pola, to pole każdego z nich to dokładnie 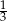 pola całego trójkąta. W takim razie, jeżeli
pola całego trójkąta. W takim razie, jeżeli 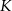 i
i 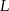 są rzutami punktu
są rzutami punktu 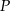 na boki
na boki 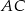 i
i 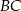 , to
, to
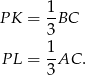
Aby nie mieć ułamków, oznaczmy 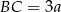 i
i 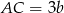 . Wtedy
. Wtedy 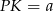 ,
, 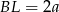 ,
, 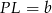 ,
, 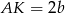 . Z twierdzenia Pitagorasa mamy równości
. Z twierdzenia Pitagorasa mamy równości
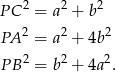
Dodając dwie ostatnie równości stronami mamy
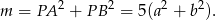
Stąd
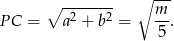
Odpowiedź: