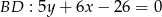/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Równoległobok

Zadanie nr 2852371

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest równoległobok 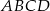ABCD o wierzchołkach 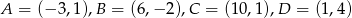A = (− 3,1),B = (6,− 2),C = (10,1),D = (1,4) . Napisz równania prostych, w których zawarte są przekątne równoległoboku.

Rozwiązanie

Zacznijmy od schematycznego rysunku.

PIC

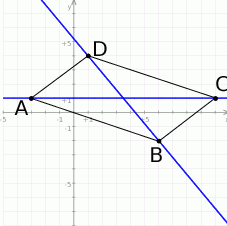
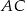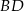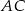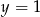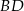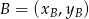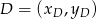Widać, że musimy napisać równania prostych AC i BD . W przypadku prostej AC sprawa jest prosta, bo oba punkty mają takie same drugie współrzędne, więc leżą na prostej y = 1 . Jeżeli chodzi o prostą BD to korzystamy na równanie prostej przechodzącej przez dwa punkty B = (xB,yB ) i D = (xD,yD ) :

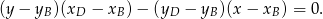
(y− yB)(xD − xB) − (yD − yB )(x− xB) = 0 .

Mamy zatem

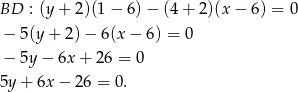
BD : (y + 2)(1 − 6)− (4+ 2)(x − 6) = 0 − 5 (y + 2 )− 6 (x− 6) = 0 − 5y − 6x+ 26 = 0 5y+ 6x − 26 = 0 .

 
Odpowiedź: 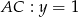AC : y = 1 , BD : 5y + 6x− 26 = 0

Wersja PDF
Rozwiązanie Losuj ponownie