Zadanie nr 9289240
W kulę o promieniu długości 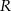 wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
Rozwiązanie
Rysujemy przekrój osiowy opisanej sytuacji.
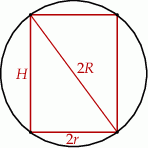
Liczymy objętość walca.
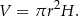
Mamy ponadto
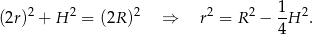
Podstawiamy to do wzoru na objętość
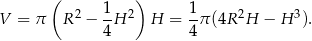
Pozostało wyznaczyć największą wartość funkcji 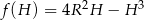 na przedziale
na przedziale 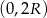 . Liczymy pochodną
. Liczymy pochodną
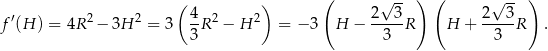
Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, zatem w przedziale 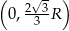 pochodna jest dodatnia, czyli
pochodna jest dodatnia, czyli 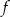 rośnie, a w przedziale
rośnie, a w przedziale 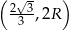 pochodna jest ujemna, czyli funkcja maleje. Największa wartość jest więc przyjmowana dla
pochodna jest ujemna, czyli funkcja maleje. Największa wartość jest więc przyjmowana dla 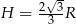 . Mamy wtedy
. Mamy wtedy
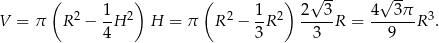
Liczymy teraz szukany iloraz
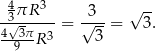
Odpowiedź: