Zadanie nr 1557231

Oblicz sumę miar kątów utworzonych przez przekątne pięciokąta wypukłego.

Rozwiązanie

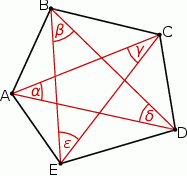
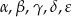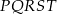Zauważmy, że przy użyciu oznaczonych kątów α,β,γ ,δ,𝜀 łatwo wyznaczyć kąty wewnętrzne pięciokąta P QRST .

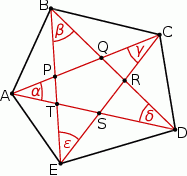
Mamy więc

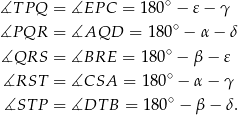
∘ ∡T PQ = ∡EP C = 180 − 𝜀 − γ ∡P QR = ∡AQD = 180∘ − α − δ ∘ ∡QRS = ∡BRE = 180 − β − 𝜀 ∡RST = ∡CSA = 180 ∘ − α − γ ∘ ∡ST P = ∡DT B = 18 0 − β− δ.

Teraz korzystamy z tego, że suma kątów w pięciokącie 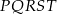P QRST jest równa

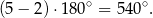
(5 − 2) ⋅180∘ = 540∘.

Mamy zatem

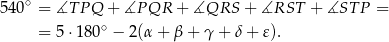
∘ 540 = ∡T P Q + ∡P QR + ∡QRS + ∡RST + ∡ST P = = 5⋅ 180∘ − 2(α + β + γ + δ + 𝜀).

Stąd

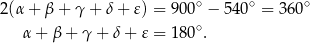
2(α+ β+ γ + δ + 𝜀) = 900∘ − 54 0∘ = 360∘ ∘ α+ β+ γ + δ + 𝜀 = 180 .

Odpowiedź: ∘ 180