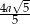Zadanie nr 3508721
W kwadrat 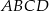 o boku długości
o boku długości 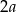 wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek
wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek 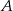 ze środkiem boku
ze środkiem boku 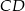 .
.
Rozwiązanie
Zacznijmy od rysunku.
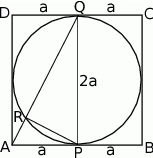
Sposób I
Trójkąt 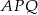 jest prostokątny oraz
jest prostokątny oraz 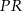 jest jego wysokością (kąt
jest jego wysokością (kąt 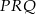 jest oparty na średnicy). W takim razie trójkąty
jest oparty na średnicy). W takim razie trójkąty 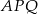 i
i 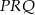 są podobne i mamy
są podobne i mamy
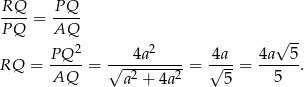
Sposób II
Stosujemy twierdzenie Pitagorasa w trójkącie prostokątnym  .
.
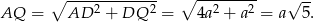
Na mocy twierdzenia o siecznych, mamy
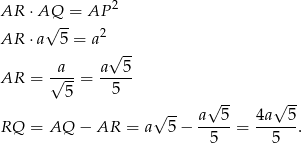
Sposób III
Tak jak poprzednio obliczamy 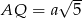 . Odcinek
. Odcinek 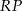 jest wysokością w trójkącie
jest wysokością w trójkącie 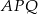 , więc
, więc
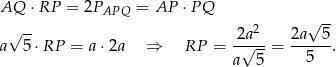
Piszemy teraz twierdzenie Pitagorasa w trójkącie 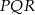 .
.
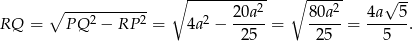
Odpowiedź: