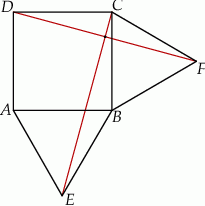
Cztery miasta  i
i  znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami
znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami  i
i  , a drugi węzeł z miastami
, a drugi węzeł z miastami  i
i  (zobacz rysunek).
(zobacz rysunek).
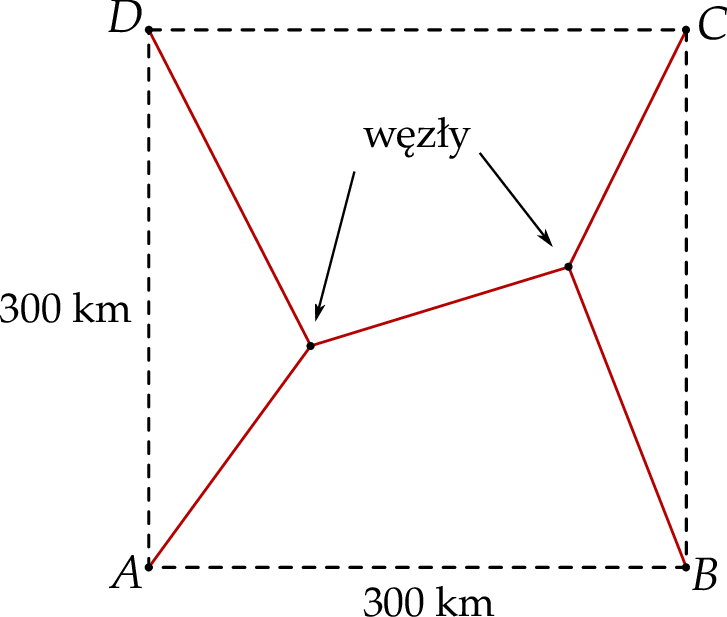
Oblicz, jaka musi być długość najkrótszej takiej sieci dróg i gdzie muszą być zlokalizowane węzły tej sieci.

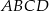 o boku długości
o boku długości 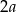 wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek
wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek 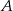 ze środkiem boku
ze środkiem boku 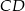 .
. 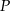 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 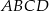 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 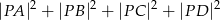 ma stałą wartość, niezależną od wyboru punktu
ma stałą wartość, niezależną od wyboru punktu 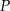 .
. 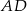 i
i 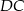 kwadratu
kwadratu 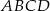 o polu 1 wybrano punkty
o polu 1 wybrano punkty 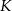 i
i 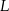 w ten sposób, że
w ten sposób, że  .
. 
 od prostej
od prostej 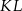 .
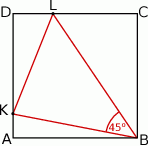
. 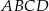 i
i 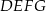 , przy czym punkty
, przy czym punkty 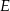 i
i 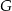 należą do odcinków
należą do odcinków 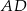 i
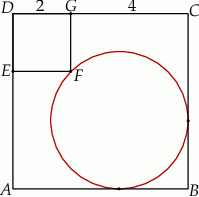
i 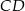 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 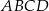 i przechodzi przez punkt
i przechodzi przez punkt 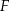 . Wykaż, że jeżeli
. Wykaż, że jeżeli 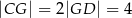 , to promień okręgu jest równy
, to promień okręgu jest równy 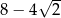 .
. 
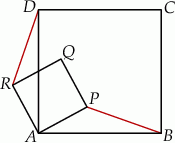
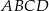 i
i 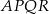 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 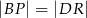 .
.
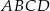 na bokach
na bokach 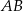 i
i 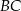 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 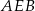 i
i 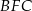 . Uzasadnij, że proste
. Uzasadnij, że proste 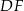 i
i 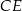 są prostopadłe.
są prostopadłe.