/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 3542824

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 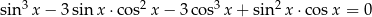3 2 3 2 sin x − 3 sinx ⋅cos x − 3co s x + sin x ⋅cos x = 0 w przedziale ⟨0 ,π⟩ .

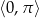Rozwiązanie

Sposób I

Przekształcamy dane równanie tak, aby spróbować zamienić lewą stronę na iloczyn.

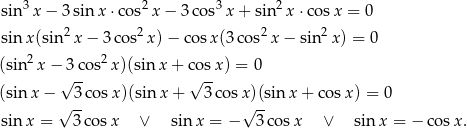
3 2 3 2 sin x − 3 sinx ⋅cos x− 3co s x + sin x ⋅cos x = 0 sinx (sin 2x − 3 cos2x) − cos x(3 cos2x − sin2x ) = 0 (sin 2x − 3 cos2x)(sin x+ cosx ) = 0 √ -- √ -- (sin x − √ 3-cosx )(sin x + 3c osx√)(sin x+ cosx ) = 0 sinx = 3co sx ∨ sin x = − 3 cosx ∨ sin x = − cosx .

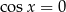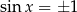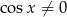Zauważmy, że jeżeli cos x = 0 , to wtedy sin x = ± 1 , więc taki x nie spełnia żadnego z powyższych równań. Możemy więc założyć, że co sx ⁄= 0 i podzielić każde z równań przez co sx .

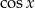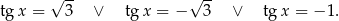
tg x = √ 3- ∨ tgx = − √ 3- ∨ tgx = − 1.

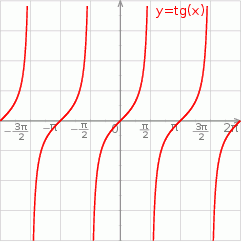
Szkicujemy tangensa.

PIC

W przedziale 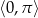⟨0,π⟩ każde z powyższych równań ma dokładnie jedno rozwiązanie. W sumie mamy więc 3 rozwiązania

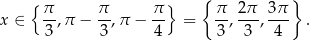
{ π π π } { π 2 π 3π } x ∈ -,π − --,π − -- = --,---, --- . 3 3 4 3 3 4

Sposób II

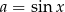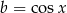Dane równanie wygląda dość nieczytelnie ze względu na dużą liczbę sinusów i cosinusów po lewej stronie. Podstawmy więc a = sin x i b = cosx .

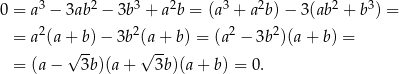
0 = a3 − 3ab2 − 3b3 + a2b = (a3 + a2b)− 3(ab2 + b3) = 2 2 2 2 = a (a+√ b)− 3b (√a+- b) = (a − 3b )(a+ b) = = (a− 3b)(a+ 3b)(a + b) = 0.

Otrzymujemy więc równanie

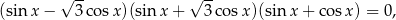
√ -- √ -- (sin x − 3 cosx)(sin x+ 3co sx)(sin x+ cosx) = 0,

które rozwiązujemy tak samo jak w I sposobie.  
Odpowiedź: { π 2π 3π} x ∈ 3, 3-,-4-

Wersja PDF
Rozwiązanie Losuj ponownie