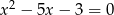Zadanie nr 2796970
Ułóż równanie kwadratowe, takie, by suma pierwiastków równania była równa 5 oraz aby kwadrat różnicy tych pierwiastków był równy 37.
Rozwiązanie
Wyliczymy wartości wyrażeń 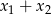 i
i 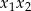 , które na mocy wzorów Viète’a dają współczynniki
, które na mocy wzorów Viète’a dają współczynniki 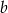 i
i  równania
równania
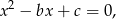
którego rozwiązaniami są 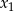 i
i 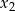 .
.
Mamy 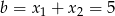 oraz
oraz
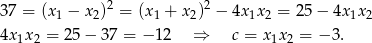
Zatem szukane równanie to 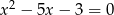 .
.
Powyżej znaleźliśmy przykład równania, o żądanych własnościach. Gdybyśmy chcieli wyznaczyć wszystkie takie równania, to musimy odpowiedź przemnożyć przez dowolne 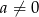 (bo ta operacja nie zmienia pierwiastków równania).
(bo ta operacja nie zmienia pierwiastków równania).
Odpowiedź: