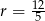Zadanie nr 5531905

W trójkąt równoramienny o podstawie 24 cm i wysokości 5 cm wpisano okrąg. Oblicz promień tego okręgu.

Rozwiązanie

Zaczynamy od rysunku.

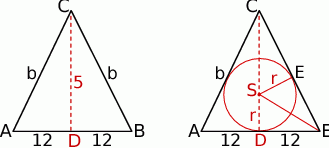
Sposób I

Obliczmy długość ramienia trójkąta oraz jego pole.

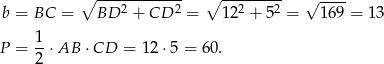
∘ ------------ ∘ --------- √ ---- b = BC = BD 2 + CD 2 = 122 + 52 = 1 69 = 13 1 P = -⋅ AB ⋅CD = 12 ⋅5 = 60 . 2

Promień okręgu wpisanego obliczymy ze wzoru na pole

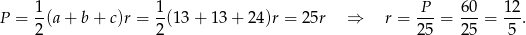
1 1 P 60 12 P = 2(a + b + c)r = 2-(13+ 13 + 24)r = 25r ⇒ r = 25-= 25-= 5-.

Sposób II

Tym razem promień okręgu wpisanego obliczymy bardziej wprost – z trójkąta prostokątnego 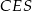CES .

Tak samo jak w pierwszym sposobie obliczamy długość ramienia trójkąta

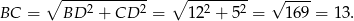
∘ ------------ ∘ --------- √ ---- BC = BD 2 + CD 2 = 1 22 + 5 2 = 169 = 1 3.

Zauważmy jeszcze, że

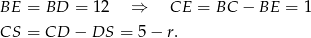
BE = BD = 1 2 ⇒ CE = BC − BE = 1 CS = CD − DS = 5− r.

Piszemy teraz twierdzenie Pitagorasa w trójkącie 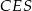CES .

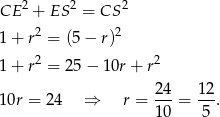
CE 2 + ES 2 = CS 2 1+ r2 = (5− r)2 2 2 1+ r = 25 − 10r + r 24- 12- 10r = 24 ⇒ r = 10 = 5 .

Sposób III

Tak samo jak w poprzednim sposobie obliczamy 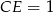CE = 1 . Teraz korzystamy z podobieństwa trójkątów 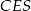CES i CDB .

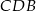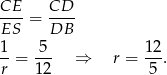
CE CD ----= ---- ES DB 1-= -5- ⇒ r = 1-2. r 1 2 5

Odpowiedź: r = 125