Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 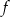 i
i 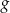 , określonych wzorami
, określonych wzorami 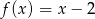 oraz
oraz 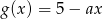 , przecinają się w punkcie o obu współrzędnych dodatnich.
, przecinają się w punkcie o obu współrzędnych dodatnich.
/Szkoła średnia/Funkcje - wykresy/Liniowy
Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 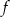 i
i 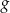 , określonych wzorami
, określonych wzorami 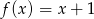 oraz
oraz 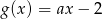 , przecinają się w punkcie o obu współrzędnych ujemnych.
, przecinają się w punkcie o obu współrzędnych ujemnych.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 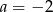 , której wykres przecina oś
, której wykres przecina oś 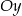 w punkcie
w punkcie 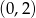 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 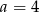 , której wykres przecina oś
, której wykres przecina oś 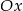 w punkcie
w punkcie 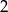 . Wyznacz punkt przecięcia wykresu z osią
. Wyznacz punkt przecięcia wykresu z osią 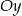 .
.
Napisz wzór funkcji liniowej, której wykres jest równoległy do wykresu funkcji 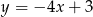 i przecina oś
i przecina oś 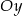 w punkcie
w punkcie 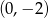 .
.
Wyznacz wzór funkcji liniowej, wiedząc że jej wykres jest nachylony do osi 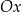 pod kątem
pod kątem 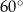 i przechodzi przez punkt
i przechodzi przez punkt 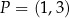 .
.
Wyznacz wzór funkcji liniowej, której wykres tworzy z osią 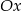 kąt
kąt 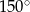 i przechodzi przez punkt
i przechodzi przez punkt 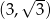 .
.
Niech 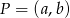 będzie dowolnym punktem wykresu funkcji
będzie dowolnym punktem wykresu funkcji 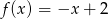 .
.
- Wyraź sumę odległości punktu
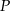 od osi układu współrzędnych jako funkcję zmiennej
od osi układu współrzędnych jako funkcję zmiennej  i naszkicuj wykres tej funkcji.
i naszkicuj wykres tej funkcji. - Znajdź współrzędne takiego punktu należącego do wykresu funkcji
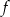 , którego suma odległości od osi układu współrzędnych jest równa 16.
, którego suma odległości od osi układu współrzędnych jest równa 16.
Podaj dla jakich wartości parametru 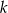 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 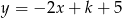 i
i 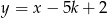 należy do koła o środku
należy do koła o środku 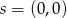 i promieniu
i promieniu 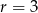 .
.

