Określ dziedzinę funkcji 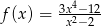 i sprowadź jej wzór do najprostszej postaci. Naszkicuj jej wykres i podaj jej zbiór wartości.
i sprowadź jej wzór do najprostszej postaci. Naszkicuj jej wykres i podaj jej zbiór wartości.
/Szkoła średnia/Funkcje - wykresy/Wymierny
Wykres funkcji 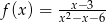 przesunięto o wektor
przesunięto o wektor ![→ u = [− 2;1]](https://img.zadania.info/zad/4272119/HzadT1x.gif) , a następnie przesunięty wykres odbito symetrycznie względem początku układu współrzędnych. Otrzymano wykres pewnej funkcji
, a następnie przesunięty wykres odbito symetrycznie względem początku układu współrzędnych. Otrzymano wykres pewnej funkcji 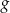 . Znajdź wzór funkcji
. Znajdź wzór funkcji 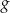 i wyznacz jej dziedzinę.
i wyznacz jej dziedzinę.
Naszkicuj wykres funkcji 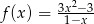 .
.
Funkcja 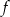 określona jest wzorem
określona jest wzorem 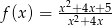 . Znajdź taki wektor
. Znajdź taki wektor ![→u = [p,0]](https://img.zadania.info/zad/8670332/HzadT2x.gif) , aby po przesunięciu wykresu funkcji
, aby po przesunięciu wykresu funkcji 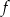 o wektor
o wektor 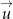 otrzymać wykres funkcji parzystej. Podaj wzór funkcji, której wykres otrzymamy po przesunięciu wykresu funkcji
otrzymać wykres funkcji parzystej. Podaj wzór funkcji, której wykres otrzymamy po przesunięciu wykresu funkcji 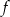 o znaleziony wektor.
o znaleziony wektor.
Rysunek przedstawia fragment wykresu funkcji 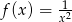 .
.
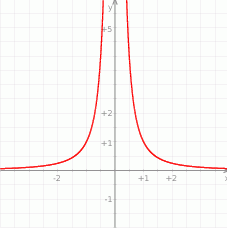
Przeprowadzono prostą równoległą do osi 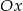 , która przecięła wykres tej funkcji w punktach
, która przecięła wykres tej funkcji w punktach 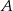 i
i 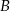 . Niech
. Niech 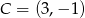 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 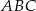 jest większe lub równe 2.
jest większe lub równe 2.

