Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej  wzorem
wzorem 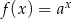 (gdzie
(gdzie 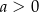 i
i 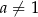 ), należy punkt
), należy punkt 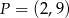 . Oblicz
. Oblicz  i zapisz zbiór wartości funkcji
i zapisz zbiór wartości funkcji 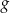 , określonej wzorem
, określonej wzorem 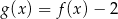 .
.
/Szkoła średnia/Funkcje - wykresy/Wykładniczy/Wzór z wykresu
Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej  wzorem
wzorem 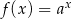 (gdzie
(gdzie 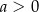 i
i 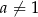 ), należy punkt
), należy punkt 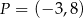 . Oblicz
. Oblicz  i zapisz zbiór wartości funkcji
i zapisz zbiór wartości funkcji 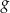 , określonej wzorem
, określonej wzorem 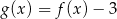 .
.
Wykres funkcji wykładniczej 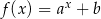 (gdzie
(gdzie 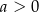 i
i 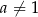 ) przesunięto o 4 jednostki w prawo i 2 jednostki w dół. W rezultacie otrzymano wykres funkcji
) przesunięto o 4 jednostki w prawo i 2 jednostki w dół. W rezultacie otrzymano wykres funkcji 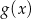 , który przecina oś
, który przecina oś 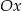 w punkcie
w punkcie 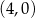 oraz przechodzi przez punkt
oraz przechodzi przez punkt 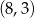 . Wyznacz
. Wyznacz  i
i 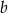 oraz rozwiąż nierówność
oraz rozwiąż nierówność 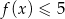 .
.
Wykres funkcji 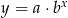 powstaje z wykresu funkcji
powstaje z wykresu funkcji 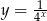 przez jednokładność o środku w punkcie
przez jednokładność o środku w punkcie 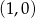 i skali
i skali 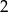 . Wyznacz liczby
. Wyznacz liczby  i
i 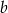 .
.
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej 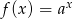 dla
dla 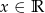
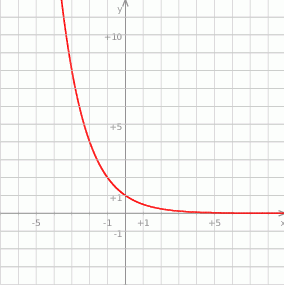
- Narysuj wykres funkcji
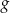 , który jest obrazem wykresu funkcji
, który jest obrazem wykresu funkcji 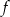 w przesunięciu o wektor
w przesunięciu o wektor ![→ u = [2,− 1]](https://img.zadania.info/zad/5083137/HzadT5x.gif) .
. - Wyznacz
 i zapisz wzór funkcji
i zapisz wzór funkcji 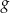 otrzymanej w wyniku tego przesunięcia.
otrzymanej w wyniku tego przesunięcia. - Odczytaj z wykresu zbiór wszystkich argumentów, dla których
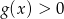 .
.
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej 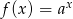 dla
dla 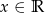 .
.
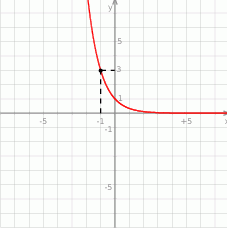
Wykres ten przekształcono w symetrii środkowej względem punktu 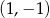 , a następnie w symetrii osiowej względem prostej
, a następnie w symetrii osiowej względem prostej 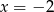 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 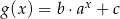 .
.
- Wyznacz liczby
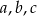 i naszkicuj wykres funkcji
i naszkicuj wykres funkcji 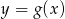 .
. - Odczytaj z wykresu rozwiązanie nierówności
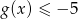 .
.

