Ile liczb trzycyfrowych podzielnych przez 9 ma następującą własność: suma cyfr ilorazu tej liczby przez 9 jest o 9 mniejsza od sumy jej cyfr?
A) 1 B) 2 C) 4 D) 5 E) 11
/Konkursy
W trójkącie równoramiennym (patrz rysunek) długość podstawy wynosi  , zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe
, zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe 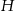 i
i 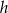 . Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę
. Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę  .
.
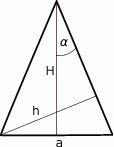
- Wyraź
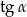 w zależności od wielkości
w zależności od wielkości  i
i 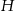 .
. - Wyraź
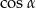 w zależności od wielkości
w zależności od wielkości  i
i 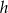 .
. - Wykaż, że jeśli
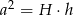 , to
, to 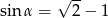 .
.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.
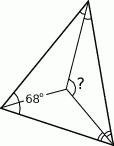
Jeden z kątów wewnętrznych trójkąta ma miarę 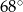 . W trójkącie tym poprowadzono dwusieczne jego kątów wewnętrznych. Ile stopni ma miara kąta zaznaczonego na rysunku znakiem zapytania?
. W trójkącie tym poprowadzono dwusieczne jego kątów wewnętrznych. Ile stopni ma miara kąta zaznaczonego na rysunku znakiem zapytania?
A) 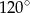 B)
B) 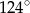 C)
C) 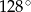 D)
D) 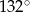 E)
E) 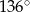
Do dwóch okręgów przecinających się w punktach 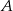 i
i 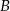 poprowadzono wspólną styczną
poprowadzono wspólną styczną 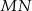 , przy czym punkt
, przy czym punkt 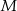 należy do pierwszego, a punkt
należy do pierwszego, a punkt 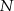 do drugiego okręgu. Wykaż, że prosta
do drugiego okręgu. Wykaż, że prosta 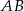 dzieli odcinek
dzieli odcinek 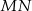 na połowy.
na połowy.
Ciąg cyfr powstał przez napisanie 2009 razy liczby 2009. Suma wszystkich cyfr nieparzystych w tym ciągu, które znajdują się bezpośrednio przed cyfrą parzystą, jest równa
A) 2 B) 9 C) 4018 D) 18072 E) 18081
Mirek ma 10 kart. Na każdej karcie jest napisana jedna z liczb: 3, 8, 13, 18, 23, 28, 33, 48, 53, 68, przy czym na każdej karcie jest inna liczba. Jaka jest najmniejsza liczba kart, które powinien wybrać Mirek, aby otrzymać sumę równą 100?
A) 2 B) 3 C) 4 D) 5 E) To jest niemożliwe
W trójkącie 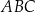 kąt
kąt 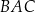 jest dwa razy większy od kąta
jest dwa razy większy od kąta 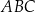 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 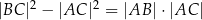 .
.
Dany jest trójkąt 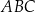 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 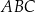 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 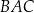 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek
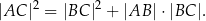
Średnica 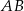 i cięciwa
i cięciwa 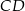 okręgu o środku
okręgu o środku 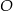 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 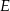 takim, że
takim, że 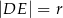 . Wykaż, że
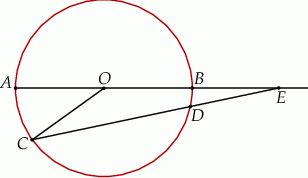
. Wykaż, że 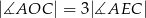 .
.
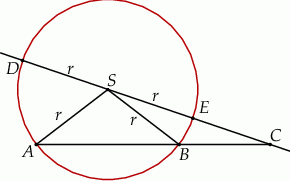
Dany jest okrąg o środku w punkcie 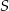 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 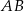 poza punkt
poza punkt 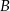 odłożono odcinek
odłożono odcinek 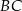 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 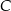 i
i 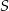 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 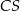 przecina dany okrąg w punktach
przecina dany okrąg w punktach 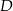 i
i 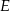 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 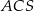 jest równa
jest równa  , to miara kąta
, to miara kąta 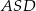 jest równa
jest równa 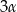 .
.
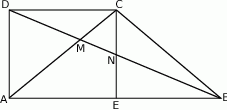
Punkt 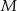 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 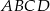 . Punkt
. Punkt 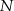 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 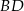 i wysokości
i wysokości 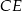 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 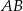 . Wykaż, że
. Wykaż, że 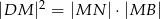 .
.
Okrąg wpisany w trójkąt 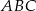 jest styczny do boków
jest styczny do boków 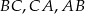 odpowiednio w punktach
odpowiednio w punktach 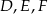 . Punkty
. Punkty 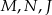 są odpo- wiednio środkami okręgów wpisanych w trójkąty
są odpo- wiednio środkami okręgów wpisanych w trójkąty 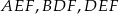 . Dowieść, że punkty
. Dowieść, że punkty 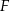 i
i 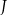 są symetryczne względem prostej
są symetryczne względem prostej 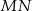 .
.
Trzy proste przecinają w jednym punkcie, jak na rysunku obok, na którym podane są również miary dwóch kątów. Jaka jest miara zacieniowanego kąta?
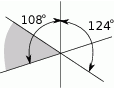
A) 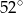 B)
B) 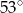 C)
C) 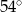 D)
D) 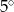 E)
E) 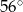
Wynikiem działania 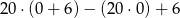 jest
jest
A) 0 B) 106 C) 114 D) 126 E) 12
Trzej robotnicy pracujący dziennie po 8 godzin wykonywali w ciągu 6 dni 40% pracy. Ilu trzeba robotników którzy pracując po 9 godzin dziennie wykonaliby resztę pracy w ciągu 4 dni?
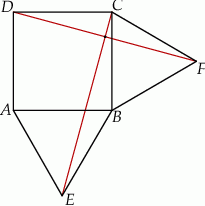
Na zewnątrz kwadratu 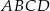 na bokach
na bokach 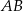 i
i 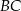 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 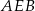 i
i 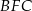 . Uzasadnij, że proste
. Uzasadnij, że proste 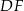 i
i 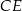 są prostopadłe.
są prostopadłe.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.

