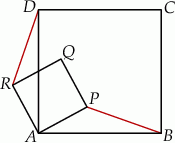
Czworokąty 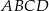 i
i 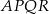 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 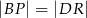 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Czworokąty 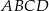 i
i 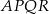 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 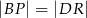 .
.

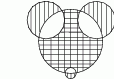
Jaką najmniejszą liczbę małych kwadracików należy zacieniować na rysunku obok, aby powstała figura miała oś symetrii?

A) 4 B) 6 C) 5 D) 2 E) 3
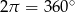 .
. 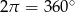 .
.  –kąta.
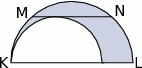
–kąta.Na rysunku obok przedstawione są dwa półokręgi oraz cięciwa 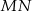 większego półokręgu, która jest równoległa do
większego półokręgu, która jest równoległa do 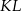 i styczna do mniejszego półokręgu. Ile wynosi pole zacieniowanego obszaru, jeżeli
i styczna do mniejszego półokręgu. Ile wynosi pole zacieniowanego obszaru, jeżeli 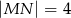 ?
?
A) 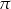 B)
B) 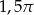 C)
C) 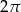 D)
D) 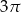 E) Za mało danych by to wyliczyć
E) Za mało danych by to wyliczyć
Pole trapezu jest równe 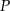 , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
, a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
Okrąg podzielono na cztery łuki o długościach 2, 5, 6 i  . Kąt środkowy oparty na łuku długości 2 ma miarę
. Kąt środkowy oparty na łuku długości 2 ma miarę 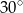 . Jaką wartość ma
. Jaką wartość ma  .
.
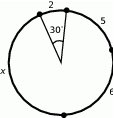
A) 7 B) 8 C) 9 D) 10 E) 11
W pięciu pudełkach znajdują się karty oznaczone literami A, E, I, O, U, jak pokazano na rysunku. Paweł powyjmował z pudełek niektóre karty tak, że w każdym z nich została jedna karta, przy czym w każdym z inną literą. Która karta pozostała w pudełku 2?
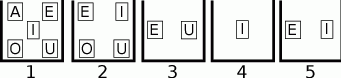
A) A B) E C) I D) O E) U
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 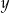 prawdziwa jest nierówność
prawdziwa jest nierówność
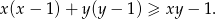
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 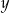 prawdziwa jest nierówność
prawdziwa jest nierówność
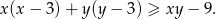
Wykaż, że jeżeli 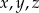 są długościami boków trójkąta to
są długościami boków trójkąta to 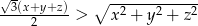 .
.
Niech 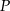 oznacza pole obszaru zakreskowanego liniami pionowymi i niech
oznacza pole obszaru zakreskowanego liniami pionowymi i niech 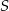 będzie polem zakreskowanej figury. Średnice kół wynoszą odpowiednio 6, 4, 4 i 2. Wówczas
będzie polem zakreskowanej figury. Średnice kół wynoszą odpowiednio 6, 4, 4 i 2. Wówczas
A) 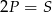 B)
B) 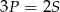 C)
C) 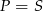 D)
D) 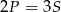 E)
E) 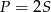
Kwadrat podzielono na 2009 kwadratów, których długości boków są liczbami całkowitymi. Jaką najmniejszą długość może mieć bok dzielonego kwadratu?
A) 44
B) 45
C) 46
D) 503
E) Nie można kwadratu podzielić na 2009 takich kwadratów.
Z którego z poniższych kawałków papieru można skleić pudełko, którego kształt przedstawiono na rysunku obok?

Jeżeli iloczyn dwóch liczb całkowitych jest równy 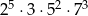 , to ich suma
, to ich suma
A) może być podzielna przez 8
B) może być podzielna przez 3
C) może być podzielna przez 5
D) może być podzielna przez 49
E) nie może być podzielna przez żadną z liczb 8, 3, 5, 49
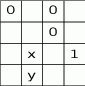
Uzupełniamy tablicę wpisując w każde pole liczbę 0 albo 1, w taki sposób, aby sumy liczb każdego wiersza i każdej kolumny były równe 2. Jakie są wartości  i
i 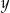 ?
?
A) 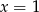 ,
, 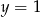 B)
B) 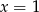 ,
, 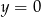 C)
C) 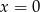 ,
, 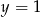 D)
D) 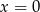 ,
, 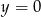 E) Nie można tego ustalić
E) Nie można tego ustalić
Ile cyfr ma w zapisie dziesiętnym liczba 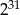 ?
?
Aby otrzymać liczbę 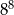 , liczbę
, liczbę 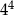 należy podnieść do potęgi
należy podnieść do potęgi
A) 2 B) 3 C) 4 D) 6 E) 16
Uzasadnić, że  prostych może podzielić płaszczyznę na maksymalnie
prostych może podzielić płaszczyznę na maksymalnie 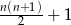 obszarów.
obszarów.
Punkt 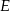 leży na ramieniu
leży na ramieniu 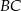 trapezu
trapezu 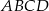 , w którym
, w którym 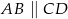 . Udowodnij, że
. Udowodnij, że 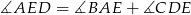 .
.
Piotr pokonuje na rowerze trasę z miasta 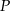 do miasta
do miasta 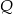 ze stałą prędkością. Gdyby zwiększył prędkość o
ze stałą prędkością. Gdyby zwiększył prędkość o 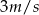 , to przybyłby do
, to przybyłby do 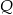 w czasie 3 razy krótszym. Ile razy krócej będzie jechał z
w czasie 3 razy krótszym. Ile razy krócej będzie jechał z 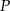 do
do 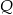 , jeżeli zwiększy prędkość o
, jeżeli zwiększy prędkość o 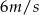 ?
?
A) 4 B) 5 C) 6 D) 4,5 E) 8
Która z poniższych liczb nie może być wartością wyrażenia 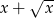 , gdzie
, gdzie  jest liczbą całkowitą?
jest liczbą całkowitą?
A) 870 B) 110 C) 90 D) 60 E) 30
