Wysokość trójkąta prostokątnego poprowadzona do przeciwprostokątnej ma długość 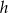 i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
/Konkursy
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych nieparzystych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez 4 jest liczbą podzielną przez 36.
Suma pewnych pięciu kolejnych liczb całkowitych jest równa sumie następnych trzech kolejnych liczb całkowitych. Największa z tych ośmiu liczb jest równa
A) 4 B) 8 C) 9 D) 11 E) 12
Odległość między środkami okręgów o promieniach 2 i 7 wynosi 13. Prosta 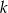 jest styczna do obu okręgów w punktach
jest styczna do obu okręgów w punktach 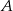 i
i 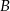 . Oblicz długość odcinka
. Oblicz długość odcinka 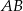 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Na poniższym rysunku przedstawiona jest oś liczbowa z zaznaczonymi kolejnymi liczbami całkowitymi. Sześć z tych liczb oznaczono literami 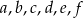 . Wiadomo, że co najmniej dwie z nich są podzielne przez 3 i co najmniej dwie z nich są podzielne przez 5. Które liczby są podzielne przez 15?
. Wiadomo, że co najmniej dwie z nich są podzielne przez 3 i co najmniej dwie z nich są podzielne przez 5. Które liczby są podzielne przez 15?
![]()
A)  i
i 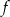 B)
B) 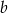 i
i  C)
C)  i
i 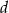 D) Wszystkie sześć E) Żadna z nich
D) Wszystkie sześć E) Żadna z nich
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
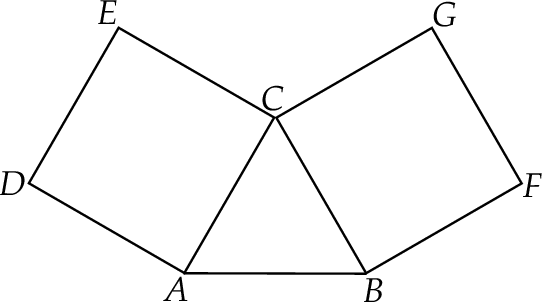
Wykaż, że punkty 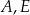 i
i 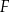 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 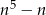 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 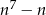 jest podzielna przez 7.
jest podzielna przez 7.
W pudełku znajduje się 7 kart. Na każdej z nich napisano dokładnie jedną z liczb od 1 do 7 i na różnych kartach, różne liczby. Mędrzec 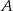 wyciągnął losowo 3 karty z pudełka, zaś mędrzec
wyciągnął losowo 3 karty z pudełka, zaś mędrzec 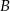 wyciągnął losowo 2 karty (w pudełku zostały dwie karty). Wówczas mędrzec
wyciągnął losowo 2 karty (w pudełku zostały dwie karty). Wówczas mędrzec 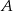 powiedział do mędrca
powiedział do mędrca 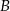 : „Wiem, że suma liczb na twoich kartach jest parzysta.” Suma liczb na kartach mędrca
: „Wiem, że suma liczb na twoich kartach jest parzysta.” Suma liczb na kartach mędrca 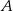 jest równa
jest równa
A) 10 B) 12 C) 6 D) 9 E) 15
Wykaż, że
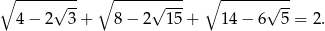
Dla jakich liczb naturalnych  , liczba
, liczba 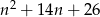 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Dla jakich liczb naturalnych  , liczba
, liczba 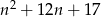 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
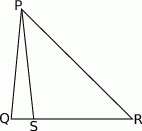
Na rysunku obok punkty 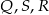 są współliniowe oraz
są współliniowe oraz 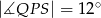 i
i 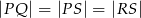 . Wówczas miara kąta
. Wówczas miara kąta 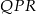 jest równa
jest równa
A) 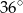 B)
B) 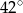 C)
C) 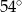 D)
D) 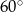 E)
E) 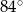
Powierzchnia bryły narysowanej obok składa się z 6 ścian trójkątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby 3 i 6 są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?
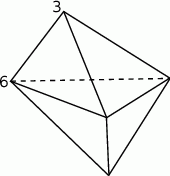
A) 9 B) 12 C) 17 D) 18 E) 24
Każdy z czterech kwadratów na rysunku ma bok długości 1. Jaka jest długość odcinka 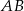 ?
?
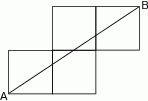
A) 5 B) 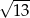 C)
C) 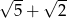 D)
D) 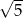 E) Inna odpowiedź
E) Inna odpowiedź
Na bokach 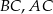 i
i 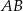 trójkąta
trójkąta 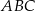 wybrano odpowiednio punkty
wybrano odpowiednio punkty 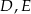 i
i 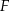 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 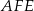 i
i 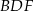 są styczne, to punkt
są styczne, to punkt 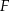 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 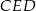 .
.
Ramiona kąta ostrego o mierze 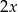 przecięto prostą
przecięto prostą 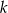 prostopadłą do dwusiecznej kąta, która jest odległa o
prostopadłą do dwusiecznej kąta, która jest odległa o 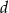 od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej
od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 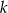 . Oblicz odległość środków tych okręgów.
. Oblicz odległość środków tych okręgów.
Trzema cięciami zaznaczonymi na rysunku podzielono duży sześcian na osiem prostopadłościanów. Ile jest równy stosunek sumy pól powierzchni tych ośmiu prostopadłościanów do pola powierzchni sześcianu?
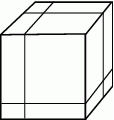
A) 1:1 B) 4:3 C) 3:2 D) 2:1 E) 4:1
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
Wykaż, że równanie 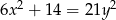 nie ma rozwiązań całkowitych.
nie ma rozwiązań całkowitych.
Ile jest liczb naturalnych  , dla których największy spośród jej dzielników naturalnych różnych od 1 i
, dla których największy spośród jej dzielników naturalnych różnych od 1 i  jest 45 razy większy od najmniejszego spośród tych dzielników?
jest 45 razy większy od najmniejszego spośród tych dzielników?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3.
W kwiaciarni są 102 róże, w tym: 24 białe, 42 czerwone i 36 żółtych. Jaka jest największa liczba jednakowych bukietów, które można ułożyć ze wszystkich róż?
A) 4 B) 6 C) 8 D) 10 E) 12

