Znajdź wzór na sumę 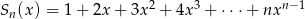 .
.
/Konkursy
Zepsuty kalkulator nie wyświetla cyfry 1. Na przykład, jeśli wpiszemy liczbę 3131, to pokazuje on liczbę 33 bez żadnych odstępów między cyframi. Michał napisał na tym kalkulatorze pewną liczbę sześciocyfrową i na wyświetlaczu kalkulatora pojawiła się liczba 2007. Dla ilu liczb mogło się tak zdarzyć?
A) 12 B) 13 C) 14 D) 15 E) 16
Uzasadnij, że jeśli 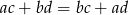 to
to 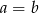 lub
lub 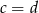 .
.
Pewna wyspa zamieszkana jest wyłącznie przez kłamców i przez rycerzy. Każdy kłamca zawsze kłamie, każdy rycerz zawsze mówi prawdę. Wyspiarz Abacki, zapytany, kim jest on i kim jest jego sąsiad Babacki, odpowiedział: „Przynajmniej jeden z nas jest kłamcą”. Które z poniższych zdań jest prawdziwe?
A) Żaden mieszkaniec wyspy nie mógł wypowiedzieć takiego zdania.
B) Obaj są kłamcami.
C) Abacki jest kłamcą, a Babacki jest rycerzem.
D) Obaj są rycerzami.
E) Abacki jest rycerzem, a Babacki jest kłamcą.
Od sześciennej drewnianej kostki odpiłowano wszystkie naroża, jak na rysunku obok. Ile krawędzi ma powstała bryła?
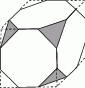
A) 48 B) 30 C) 24 D) 40 E) 36
Cyfrą jedności pewnej liczby trzycyfrowej jest 2. Jeżeli cyfrę tę przeniesiemy na początek tej liczby, to otrzymamy liczbę trzycyfrową o 36 mniejszą. Jaka jest suma cyfr tej liczby?
A) 1 B) 10 C) 7 D) 9 E) 5
Kasia rozłożyła 2007 pionków po równo do trzech pudełek 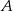 ,
, 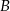 i
i 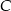 . Jeśli Kasia przełoży
. Jeśli Kasia przełoży  pionków z pudełka
pionków z pudełka 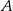 do pudełka
do pudełka 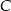 , to stosunek liczby pionków w pudełku
, to stosunek liczby pionków w pudełku 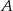 do liczby pionków w pudełku
do liczby pionków w pudełku 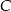 będzie równy
będzie równy
A) 1:2 B) 1:3 C) 2:3 D) 3:2 E) 1:5
Wielomian 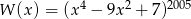 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 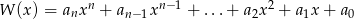 . Oblicz sumę
. Oblicz sumę 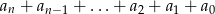 .
.
Dana jest liczba całkowita 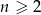 . Niech
. Niech 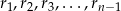 będą odpowiednio resztami z dzielenia liczb
będą odpowiednio resztami z dzielenia liczb
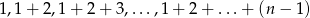
przez  . Znaleźć wszystkie takie wartości
. Znaleźć wszystkie takie wartości  , że ciąg
, że ciąg 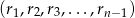 jest permutacją ciągu
jest permutacją ciągu 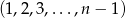 .
.
Dane są różne liczby pierwsze 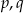 oraz takie dodatnie liczby całkowite
oraz takie dodatnie liczby całkowite 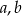 , że liczba
, że liczba 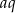 daję resztę 1 przy dzieleniu przez
daję resztę 1 przy dzieleniu przez 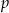 , a liczba
, a liczba 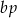 daje resztę 1 przy dzieleniu przez
daje resztę 1 przy dzieleniu przez 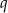 . Wykaż, że
. Wykaż, że
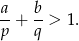
Halina narysowała kwadrat o wymiarach 5x5 i zaznaczyła na rysunku środki kwadracików jednostkowych. Następnie umieściła przeszkody (pogrubione linie – patrz rysunek) i badała, na ile sposobów można przejść od punktu 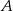 do punktu
do punktu 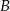 najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?
najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?

A) 6 B) 8 C) 9 D) 11 E) 12
Podstawy trapezu 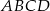 mają długości
mają długości 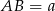 i
i 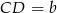 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 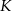 i
i 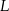 w ten sposób, że odcinek
w ten sposób, że odcinek 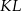 jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka
jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka 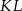 .
.
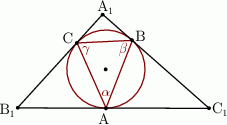
Boki trójkąta 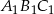 są styczne do okręgu w punktach
są styczne do okręgu w punktach 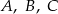 , a kąty trójkąta
, a kąty trójkąta 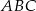 są odpowiednio równe
są odpowiednio równe 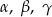 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta  .
.
W spotkaniu towarzyskim u Adama wzięło udział czterech chłopców i cztery dziewczyny. W czasie spotkania chłopcy tańczyli tylko z dziewczętami, a dziewczęta tylko z chłopcami. Po spotkaniu na pytanie: „z iloma różnymi osobami tańczyłeś w czasie spotkania”, chłopcy kolejno powiedzieli 3,1,2,2, natomiast trzy pierwsze dziewczęta podały liczby: 2,2,2. Z iloma chłopcami tańczyła czwarta dziewczyna?
A) 0 B) 1 C) 2 D) 3 E) 4
Kuba pożyczył od taty samochód, którym wyruszył z domu na spotkanie ze swoją dziewczyną. Przed wyjazdem obliczył, że jadąc ze średnią prędkością 60 km/h przybędzie na spotkanie dokładnie o umówionej godzinie. Po przejechaniu (z zaplanowaną prędkością) 60% drogi "złapał gumę", a zmiana koła zajęła mu 16 minut. Teraz, aby zdążyć na spotkanie, musiałby jechać z prędkością 120 km/h. Oblicz odległość od domu Kuby do miejsca spotkania z ukochaną.
Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach 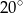 i
i 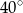 . Oblicz miary kątów czworokąta.
. Oblicz miary kątów czworokąta.
Wyznacz wszystkie liczby pierwsze 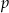 takie, że liczby
takie, że liczby 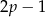 i
i 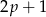 też są liczbami pierwszymi.
też są liczbami pierwszymi.
W parku wzdłuż alejki o długości 20m postanowiono po obu jej stronach posadzić krzewy róż. Zachowano przy tym zasadę, że odległość pomiędzy każdymi sąsiednimi krzewami po każdej stronie alejki jest równa 2m. Jaką maksymalną liczbę krzewów można posadzić wzdłuż tej alejki?
A) 22 B) 20 C) 12 D) 11 E) 10
Prosta 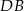 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 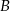 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 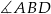 jeśli
jeśli 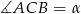 .
.
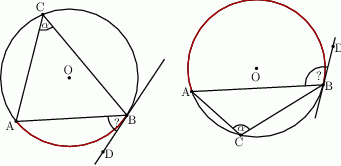
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 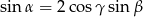 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.

