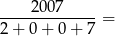
A) 1003 B) 75 C) 223 D) 213 E) 123
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
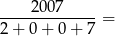
A) 1003 B) 75 C) 223 D) 213 E) 123
Mechaniczny kangurek porusza się po polach planszy przedstawionej obok na rysunku, startując z pola A3 w kierunku wskazanym strzałką. Kangurek porusza się tylko do przodu, przeskakując w pojedynczym skoku ze środka kratki, w której się znajduje, w środek kratki sąsiedniej (kratki są sąsiednie, gdy mają wspólny bok). Kangurek nie może wyskoczyć poza planszę, ani nie może wskoczyć na pola zacieniowane. Jeśli nie może wykonać skoku do przodu, to wykonuje obrót o 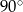 w prawo i porusza się dalej. Jeżeli po obrocie nie może wykonać skoku, to kończy wędrówkę. Na jakim polu zatrzyma się kangurek?
w prawo i porusza się dalej. Jeżeli po obrocie nie może wykonać skoku, to kończy wędrówkę. Na jakim polu zatrzyma się kangurek?

A) B2 B) A1 C) E1 D) D1 E) nigdy się nie zatrzyma
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Trapez równoramienny 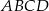 o podstawach
o podstawach 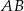 i
i 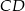 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 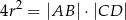 .
.
W trójkacie 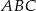 dwusieczna kąta
dwusieczna kąta 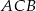 przecina bok
przecina bok 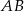 w punkcie
w punkcie 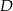 . Długosci boków
. Długosci boków 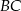 i
i 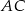 są równe odpowiednio
są równe odpowiednio  i
i 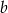 , a długość odcinka
, a długość odcinka 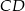 jest równa
jest równa 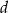 . Wykaż, że
. Wykaż, że 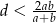 .
.
Dla pewnej liczby naturalnej  zachodzi równość
zachodzi równość
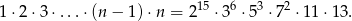
Ile wynosi  ?
?
A) 13 B) 14 C) 15 D) 16 E) 17
Jedna ze ścian sześcianu została rozcięta wzdłuż przekątnych, jak na rysunku obok. Dwa z podanych poniżej rysunków nie przedstawiają siatki tego sześcianu. Które?

A) 1 i 3 B) 1 i 5 C) 3 i 4 D) 3 i 5 E) 2 i 4
Na rysunku obok przedstawiony jest kwadrat 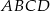 o boku długości 1 oraz łuki okręgów o środkach
o boku długości 1 oraz łuki okręgów o środkach 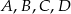 .
.
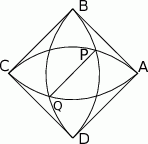
Ile wynosi długość odcinka 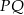 ?
?
A) 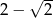 B)
B)  C)
C) 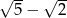 D)
D) 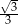 E)
E) 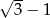
Wyznacz wszystkie liczby pierwsze 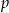 i liczby naturalne
i liczby naturalne  spełniające równość
spełniające równość
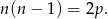
Ile nieujemnych liczb całkowitych mniejszych od 100 można otrzymać jako sumę dziewięciu kolejnych liczb całkowitych?
A) 13 B) 12 C) 11 D) 10 E) 9
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4 cm.
Brytyjski matematyk August de Morgan twierdził, że miał  lat w roku
lat w roku 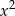 . Wiadomo, że de Morgan umarł w roku 1899. W którym roku się urodził?
. Wiadomo, że de Morgan umarł w roku 1899. W którym roku się urodził?
A) 1806 B) 1848 C) 1849 D) 1899 E) Inna odpowiedź
Wykaż, że jeżeli wielomian 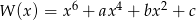 jest podzielny przez trójmian
jest podzielny przez trójmian 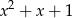 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 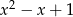 .
.
Wielomian 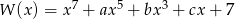 jest podzielny przez wielomian
jest podzielny przez wielomian 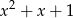 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 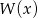 przez wielomian
przez wielomian 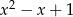 .
.
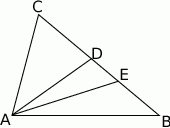
Na boku 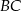 trójkąta
trójkąta 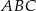 wybrano punkt
wybrano punkt  tak, by
tak, by 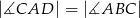 . Odcinek
. Odcinek 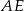 jest dwusieczną kąta
jest dwusieczną kąta 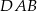 . Udowodnij, że
. Udowodnij, że 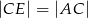 .
.
W sześcianie odcięto wszystkie naroża w sposób pokazany na rysunku obok. Ile ścian ma otrzymany w ten sposób wielościan?
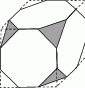
A) 10 B) 18 C) 12 D) 16 E) 14
W trójkącie 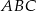 punkt
punkt 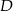 jest środkiem boku
jest środkiem boku 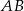 , punkt
, punkt 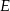 środkiem odcinka
środkiem odcinka 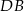 , a
, a 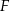 środkiem boku
środkiem boku 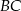 . Jeśli pole trójkąta
. Jeśli pole trójkąta 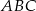 jest równe 96, to pole trójkąta
jest równe 96, to pole trójkąta 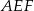 jest równe
jest równe
A) 16 B) 24 C) 32 D) 36 E) 48
Franek i Andrzej ukończyli bieg na 200 metrów. Andrzej przebiegł ten dystans w pół minuty, a Franek w setną część godziny. Kto był szybszy i o ile sekund?
A) Andrzej, o 36 sekund
B) Franek, o 24 sekund
C) Andrzej, o 6 sekund
D) Franek, o 6 sekund
E) Obaj mieli równy czas
Wartość wyrażenia 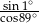 jest równa
jest równa
A) 0 B) 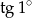 C)
C) 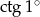 D)
D) 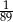 E)
E) 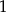
Mama przygotowała na zimę sok wiśniowy, którym można napełnić dokładnie 12 dużych słoików albo dokładnie 20 mniejszych słoików. Mama napełniła już 9 dużych słoików i resztę postanowiła rozlać do mniejszych słoików. Ile takich słoików napełni pozostałym sokiem?
A) 3 B) 4 C) 5 D) 6 E) 8
Niech 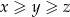 będą dodatnimi liczbami rzeczywistymi takimi, że
będą dodatnimi liczbami rzeczywistymi takimi, że 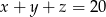 . Które z poniższych zdań jest prawdziwe?
. Które z poniższych zdań jest prawdziwe?
A) Zawsze 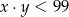
B) Zawsze 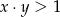
C) Zawsze 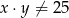
D) Zawsze 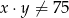
E) Żadne z poprzednich zdań nie jest prawdziwe.
W trójkącie 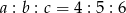 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 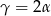 .
.
