Wyznacz w zależności od parametru  liczbę rozwiązań układu równań
liczbę rozwiązań układu równań
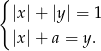
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz w zależności od parametru  liczbę rozwiązań układu równań
liczbę rozwiązań układu równań
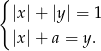
Pole przekroju ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej rozłącznej z tą przekątną wynosi  . Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
Punkt 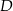 leży na boku
leży na boku 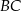 trójkąta równoramiennego
trójkąta równoramiennego 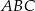 , w którym
, w którym 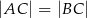 .
.
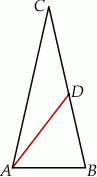
Odcinek 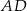 dzieli trójkąt
dzieli trójkąt 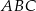 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 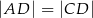 oraz
oraz 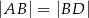 . Udowodnij, że
. Udowodnij, że 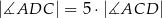 .
.
Punkt 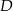 leży na boku
leży na boku 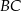 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 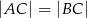 . Odcinek
. Odcinek 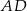 dzieli trójkąt
dzieli trójkąt 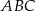 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 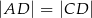 i
i 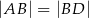 . Wykaż, że
. Wykaż, że 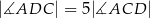 .
.
Turnieju tenisowego rozgrywanego systemem każdy z każdym nie ukończyło dwóch graczy. Jeden z nich rozegrał tylko jeden mecz, a drugi dziesięć meczy. Ilu zawodników przystąpiło do turnieju, jeżeli wiadomo, że rozegrano 55 meczy? Czy zawodnicy, którzy nie ukończyli turnieju rozegrali ze sobą mecz?
Kąty w trójkącie mają miary: 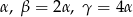 . Wykaż, że długości boków
. Wykaż, że długości boków 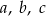 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 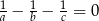 .
.
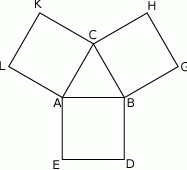
Na bokach trójkąta równobocznego 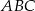 (na zewnątrz tego trójkąta) zbudowano kwadraty
(na zewnątrz tego trójkąta) zbudowano kwadraty 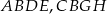 i
i 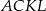 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 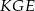 jest równoboczny.
jest równoboczny.
Dwa okręgi są styczne zewnętrznie w punkcie 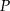 . Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach
. Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach 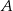 i
i 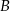 (
(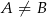 ). Wykaż, że kąt
). Wykaż, że kąt 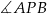 jest prosty.
jest prosty.
Dwa okręgi są zewnętrznie styczne w punkcie 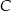 oraz są styczne do prostej
oraz są styczne do prostej 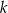 w punktach
w punktach 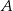 i
i 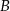 odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek).
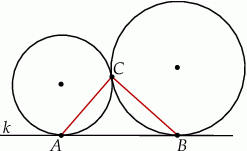
Uzasadnij, że trójkąt 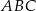 jest prostokątny.
jest prostokątny.
Złotnik miał dwa stopy złota ze srebrem. W pierwszym stopie stosunek masy złota do srebra wynosił 2:3, a w drugim 3:7. Ile musi wziąć każdego z tych stopów, aby otrzymać 8 kg nowego stopu, w którym stosunek masy złota do srebra wynosiłby 5:11?
Udowodnić, że dla dowolnych nieujemnych liczb rzeczywistych 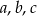 prawdziwa jest nierówność
prawdziwa jest nierówność
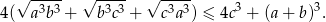
Jaka jest najmniejsza liczba 10-cyfrowa, którą można utworzyć przez dopisanie do siebie w dowolnej kolejności sześciu liczb: 309, 41, 5, 7, 68 i 2?
A) 1 234 567 890
B) 1 023 456 789
C) 3 097 568 241
D) 2 309 415 687
E) 2 309 416 857
Na płaszczyźnie dany jest kwadrat 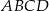 o boku długości 1. Rozważamy wszystkie kwadraty, które mają przynajmniej dwa wierzchołki wspólne z kwadratem
o boku długości 1. Rozważamy wszystkie kwadraty, które mają przynajmniej dwa wierzchołki wspólne z kwadratem 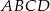 . Jakie jest pole obszaru pokrytego przez te kwadraty?
. Jakie jest pole obszaru pokrytego przez te kwadraty?
A) 5 B) 6 C) 7 D) 8 E) 9
Pięć kotów zjada pięć myszy w ciągu pięciu minut. Ile kotów zje dziesięć myszy w ciągu dziesięciu minut?
Iloma zerami kończy się dziesiętny zapis iloczynu dziesięciu początkowych liczb pierwszych?
A) 0 B) 1 C) 2 D) 3 E) 4
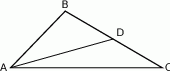
W trójkącie 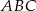 poprowadzono środkową
poprowadzono środkową 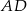 . Kąt
. Kąt 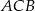 ma miarę
ma miarę 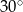 , a kąt
, a kąt 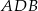 ma miarę
ma miarę 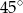 . Jaka jest miara kąta
. Jaka jest miara kąta 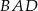 ?
?
A) 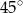 B)
B) 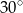 C)
C) 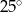 D)
D) 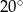 E)
E) 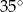
Oblicz jaka może być najmniejsza możliwa długość boku 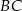 trójkąta
trójkąta 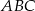 jeżeli
jeżeli 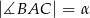 i pole trójkąta
i pole trójkąta 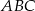 jest równe
jest równe 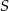 .
.
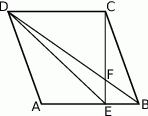
Przekątna 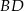 rombu
rombu 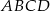 przecina jego wysokość
przecina jego wysokość 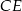 , poprowadzoną na bok
, poprowadzoną na bok 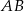 , w punkcie
, w punkcie 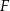 . Oblicz pole rombu
. Oblicz pole rombu 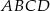 , jeśli wiadomo, że
, jeśli wiadomo, że 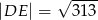 oraz
oraz 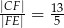 .
.
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
Dla ilu wartości rzeczywistych parametru  równanie
równanie 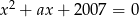 ma dwa rozwiązania całkowitoliczbowe?
ma dwa rozwiązania całkowitoliczbowe?
A) 3 B) 4 C) 6 D) 8 E) 2007
W liczbie, o której wiadomo, że miała, co najmniej dwie cyfry, wykreślono ostatnią cyfrę. Otrzymana liczba była,  razy mniejsza od poprzedniej. Jaka jest największa możliwa wartość
razy mniejsza od poprzedniej. Jaka jest największa możliwa wartość  ?
?
Dodatnia liczba naturalna  ma dwa dzielniki naturalne, podczas gdy liczba
ma dwa dzielniki naturalne, podczas gdy liczba 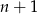 ma trzy dzielniki naturalne. Ile dzielników naturalnych ma liczba
ma trzy dzielniki naturalne. Ile dzielników naturalnych ma liczba 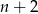 ?
?
A) 2 B) 3 C) 4 D) 5 E) Zależy to od 
