Pięcioro przyjaciół zamierza na przyjęciu dać sobie nawzajem prezenty w taki sposób, że każdy da tylko jednej osobie prezent, i każdy otrzyma prezent tylko od jednej osoby (oczywiście nikt nie daje prezentu sobie). Na ile sposobów można to zrobić?
A) 5 B) 10 C) 44 D) 50 E) 120
/Konkursy
Ile par liczb 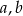 ze zbioru
ze zbioru 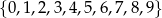 spełnia równanie
spełnia równanie 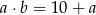 ?
?
A) 0 B) 1 C) 2 D) 3 E) 4
Jaka jest najmniejsza liczba liter, które należy usunąć ze słowa KANGOUROU, aby otrzymać słowo, w którym litery się nie powtarzają i stoją w kolejności alfabetycznej?
A) 1 B) 2 C) 3 D) 4 E) 5
Podczas rozwiązywania jednego z zadań kangurowych Basia zauważyła, że prawdziwe są następujące zdania:
- Jeśli odpowiedź
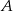 jest prawdziwa, to odpowiedź
jest prawdziwa, to odpowiedź 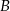 także jest prawdziwa.
także jest prawdziwa. - Jeśli odpowiedź
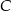 nie jest prawdziwa, to odpowiedź
nie jest prawdziwa, to odpowiedź 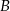 także nie jest prawdziwa.
także nie jest prawdziwa. - Jeśli odpowiedź
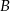 nie jest prawdziwa, to ani odpowiedź
nie jest prawdziwa, to ani odpowiedź 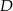 , ani
, ani 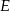 nie jest prawdziwa.
nie jest prawdziwa.
Którą odpowiedź powinna wybrać Basia?
A) A B) B C) C D) D E) E
W pewnym miesiącu trzy wtorki wypadły w parzyste dni tego miesiąca. Jakim dniem tygodnia będzie dwudziesty pierwszy dzień tego miesiąca?
A) Niedziela B) Sobota C) Piątek D) Czwartek E) Środa
Dany jest okrąg 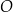 . Przez punkt
. Przez punkt 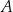 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 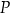 oraz
oraz 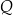 . Przez punkt
. Przez punkt 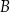 leżący na odcinku
leżący na odcinku 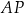 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie  , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek).
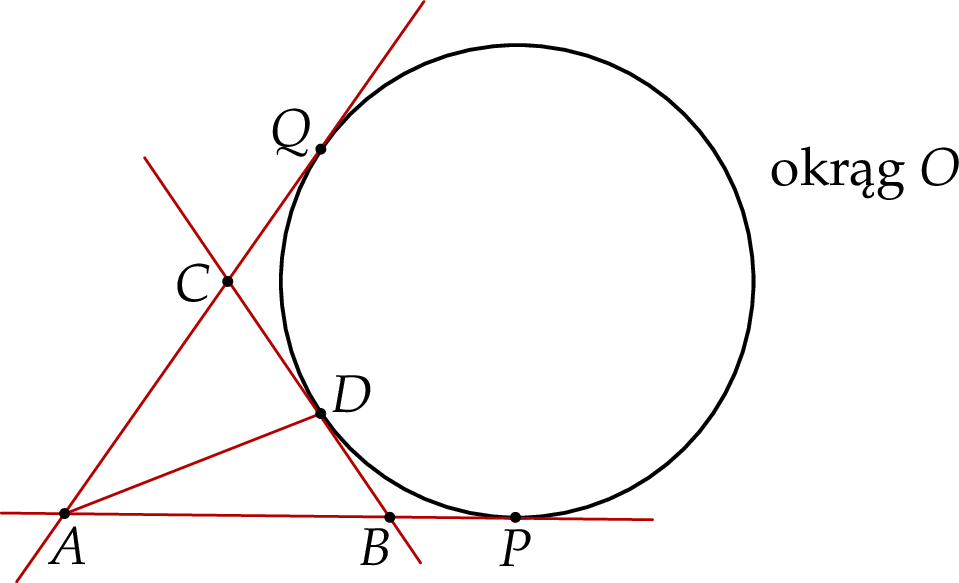
Wykaż, że jeżeli 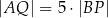 oraz
oraz 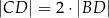 , to trójkąt
, to trójkąt  jest równoramienny.
jest równoramienny.
Dany jest okrąg 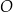 . Przez punkt
. Przez punkt  poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 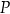 oraz
oraz 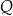 . Przez punkt
. Przez punkt 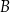 leżący na odcinku
leżący na odcinku 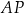 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 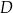 , która przecięła odcinek
, która przecięła odcinek 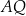 w punkcie
w punkcie 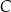 (zobacz rysunek).
(zobacz rysunek).
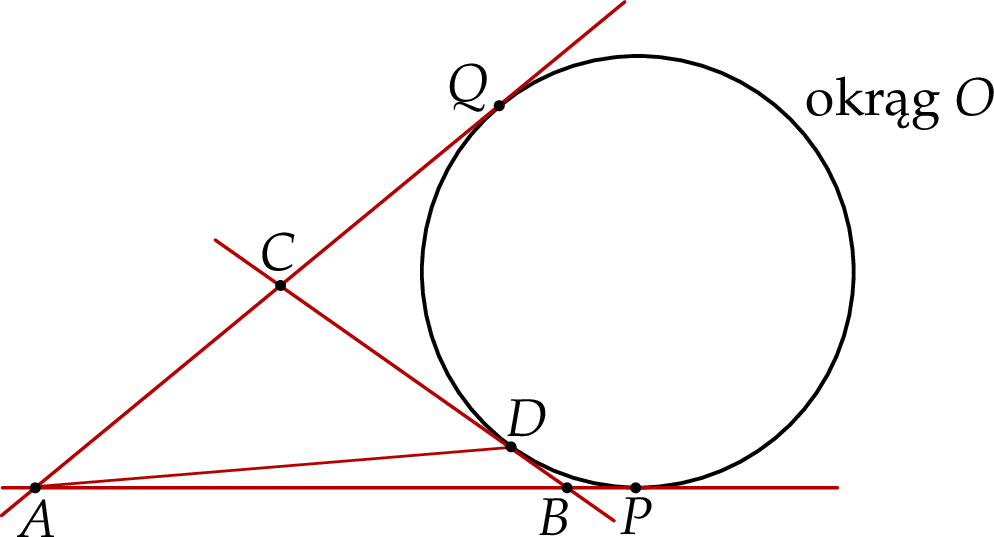
Wykaż, że jeżeli 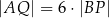 oraz
oraz 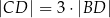 , to trójkąt
, to trójkąt 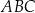 nie jest równoramienny.
nie jest równoramienny.
Niech 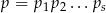 będzie liczbą całkowitą o cyfrach
będzie liczbą całkowitą o cyfrach 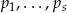 . Pokaż, że
. Pokaż, że
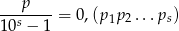
(okresowe rozwinięcie dziesiętne).
Organizacja międzynarodowa liczy 32 członków. Ilu członków będzie liczyła ta organizacja po 3 latach, jeśli rokrocznie ich liczba wzrasta o 50%?
A) 182 B) 128 C) 108 D) 96 E) 80
Dla jakich liczb całkowitych  liczba
liczba 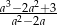 jest także liczbą całkowitą?
jest także liczbą całkowitą?
Na osi liczbowej zaznaczono ułamki 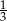 i
i 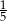 .
.
![]()
Która z liter oznacza ułamek 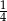 ?
?
A)  B)
B) 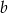 C)
C)  D)
D) 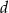 E)
E) 
Znajdź wszystkie funkcje 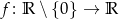 , dla których zachodzi równość
, dla których zachodzi równość 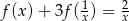 .
.
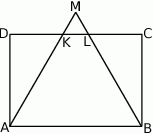
Dany jest prostokąt 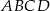 , w którym
, w którym 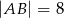 i
i 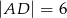 . Na boku
. Na boku 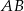 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 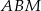 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta 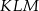 .
.
Funkcja 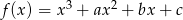 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe:  . Wykaż, że
. Wykaż, że
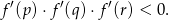
Na rysunku przedstawiony jest fragment wykresu funkcji 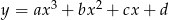 . Ile wynosi
. Ile wynosi  ?
?
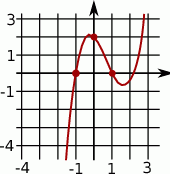
A) -4 B) -2 C) 0 D) 2 E) 4
Ramiona trapezu są średnicami dwóch okręgów. Wykaż, że jeśli okręgi te są styczne zewnętrznie, to w trapez ten można wpisać okrąg.
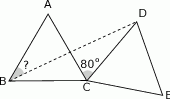
Na rysunku obok trójkąty  i
i 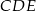 są równoboczne i przystające. Jaka jest miara kąta
są równoboczne i przystające. Jaka jest miara kąta 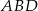 jeżeli miara kąta
jeżeli miara kąta 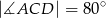 ?
?
A) 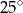 B)
B) 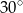 C)
C) 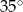 D)
D) 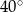 E)
E) 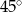
Butelka o pojemności 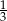 litra jest w
litra jest w  swojej pojemności wypełniona sokiem. Ile soku pozostanie w butelce po odlaniu
swojej pojemności wypełniona sokiem. Ile soku pozostanie w butelce po odlaniu 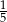 litra?
litra?
A) 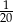 litra B)
litra B) 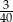 litra C) 0,13 litra D)
litra C) 0,13 litra D)  litra E) Butelka będzie pusta
litra E) Butelka będzie pusta
Na niektórych polach szachownicy rozmiaru 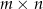 ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od
ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od 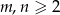 , największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
, największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
Przez punkt 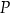 leżący na zewnątrz okręgu poprowadzono styczną i sieczną do tego okręgu. Styczna przecina ten okrąg w punkcie
leżący na zewnątrz okręgu poprowadzono styczną i sieczną do tego okręgu. Styczna przecina ten okrąg w punkcie  , a sieczna w punktach
, a sieczna w punktach  i
i  .
.
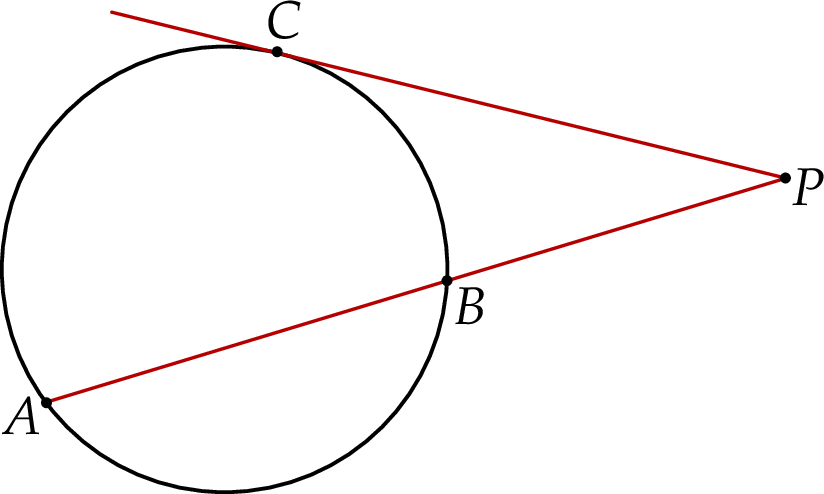
Wykaż, że
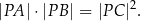
(Jest to tzw. twierdzenie o stycznej i siecznej.)
Okrąg podzielono dwudziestoma punktami na dwadzieścia łuków tej samej długości. Ile można zbudować łamanych zamkniętych z wierzchołkami w tych punktach i z odcinkami równej długości? (Odcinki mogą się przecinać, ale nie mogą się pokrywać.)

