Które z poniższych figur przedstawiają bryłę z rysunku obok?
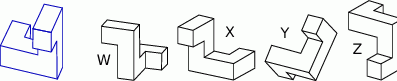
A) W oraz Y B) X oraz Z C) Tylko Y D) Żadna z nich E) W, X oraz Y
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Które z poniższych figur przedstawiają bryłę z rysunku obok?

A) W oraz Y B) X oraz Z C) Tylko Y D) Żadna z nich E) W, X oraz Y
Wykaż, że jeśli 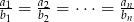 i
i 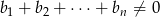 , to
, to 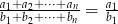 .
.
Jeżeli każdy z wierzchołków 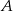 i
i 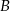 trójkąta
trójkąta 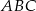 połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków
połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków 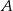 i
i 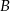 połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
A) 16 B) 25 C) 36 D) 42 E) 49
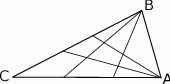
Ile kwadratów można narysować, łącząc odcinkami kropki na rysunku obok?

A) 2 B) 3 C) 4 D) 5 E) 6
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 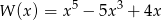 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
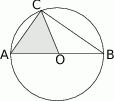
Na trójkącie 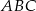 opisano okrąg o środku
opisano okrąg o środku 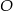 (rysunek obok). Zacieniowany trójkąt ma pole równe
(rysunek obok). Zacieniowany trójkąt ma pole równe 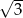 . Ile jest równe pole trójkąta
. Ile jest równe pole trójkąta 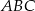 ?
?
A) 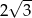 B)
B) 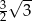 C)
C) 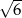 D)
D) 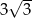 E)
E) 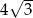
Odcinając narożnik danego trójkąta równobocznego, otrzymano trapez. Gdy ułożymy z dwóch takich trapezów równoległobok, to jego obwód jest o 10 cm większy od obwodu tego trójkąta równobocznego. Jaki jest obwód danego trójkąta równobocznego?
A) 10 cm B) 30 cm C) 40 cm D) 60 cm E) Mamy za mało informacji, żeby to obliczyć
Styczna w punkcie 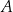 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 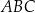 przecina prostą
przecina prostą 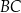 w punkcie
w punkcie 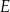 . Niech
. Niech 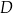 będzie punktem przecięcia dwusiecznej kąta
będzie punktem przecięcia dwusiecznej kąta 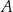 z prostą
z prostą 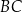 . Udowodnić, że
. Udowodnić, że 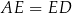 .
.
Kolejne wyrazy ciągu 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9... wpisujemy spiralnie w kratki nieskończonego diagramu, tak jak na rysunku obok. Jaką liczbę wpiszemy w setnej kratce ponad kratką zacieniowaną?
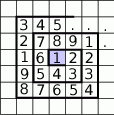
A) 8 B) 5 C) 6 D) 1 E) 3
Na bokach 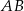 i
i 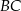 prostokąta
prostokąta 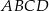 wybrano punkty
wybrano punkty 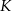 i
i 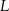 w ten sposób, że trójkąt
w ten sposób, że trójkąt 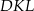 jest ostrokątny oraz
jest ostrokątny oraz 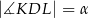 . Odcinek
. Odcinek 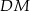 jest wysokością trójkąta
jest wysokością trójkąta 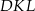 .
.
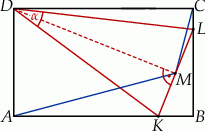
Wykaż, że 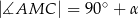 .
.
Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.
Przez każde dwa sąsiednie wierzchołki czworokąta 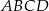 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
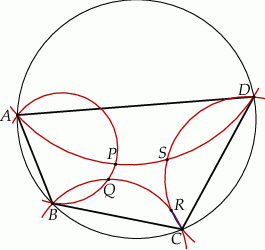
Wykaż, że punkty 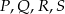 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Wykaż, że 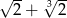 jest liczbą niewymierną.
jest liczbą niewymierną.
W trójkąt równoboczny wpisane są 3 koła o równych promieniach, przy czym każde koło jest styczne do dwóch boków trójkąta oraz do dwóch pozostałych kół. Oblicz stosunek sumy pól tych kół do pola trójkąta.
W trójkącie 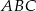 , o bokach długości
, o bokach długości 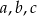 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 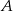 z punktem
z punktem 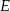 na boku
na boku 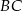 takim, że
takim, że 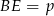 i
i 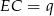 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 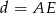 , to
, to 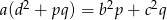 (twierdzenie Stewarta).
(twierdzenie Stewarta).
Liczby dodatnie 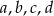 i
i  są takie, że
są takie, że 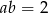 ,
, 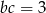 ,
, 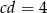 ,
, 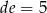 . Jaką wartość ma
. Jaką wartość ma 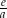 ?
?
A) 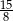 B)
B)  C)
C)  D)
D) 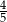 E) Wartości tej nie można wyznaczyć
E) Wartości tej nie można wyznaczyć
Udowodnij, że dla dowolnych liczb 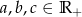 zachodzi nierówność
zachodzi nierówność
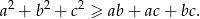
Punkt 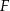 jest środkiem boku
jest środkiem boku 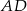 prostokąta
prostokąta 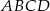 , w którym
, w którym 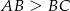 . Punkt
. Punkt 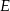 jest takim punktem boku
jest takim punktem boku 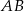 tego prostokąta, że prosta
tego prostokąta, że prosta 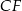 jest dwusieczną kąta
jest dwusieczną kąta 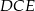 . Wykaż, że trójkąt
. Wykaż, że trójkąt 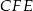 jest prostokątny.
jest prostokątny.
Iloczyn trzech liczb pierwszych jest pięć razy większy od ich sumy. Wyznacz te liczby.
Jaka jest pierwsza cyfra najmniejszej liczby naturalnej, której suma cyfr jest równa 2006?
A) 1 B) 3 C) 5 D) 6 E) 8
