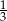Wykaż, że jeżeli 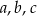 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 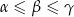 to
to 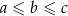 .
.
/Konkursy
Na okręgu rozmieszczono liczby: 1,2,3. Pomiędzy każde dwie sąsiednie liczby wpisano ich sumy, otrzymując na okręgu sześć liczb 1,3,2,5,3,4. Operację wpisywania sum liczb sąsiednich powtórzono jeszcze trzy razy. W rezultacie otrzymano na okręgu 48 liczb. Ile wynosi ich suma?
A) 162 B) 1458 C) 486 D) 144 E) 210
Niech  będzie liczbą naturalną, a
będzie liczbą naturalną, a  i
i 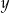 dodatnimi liczbami rzeczywistymi takimi, że
dodatnimi liczbami rzeczywistymi takimi, że 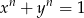 . Udowodnij nierówność:
. Udowodnij nierówność:
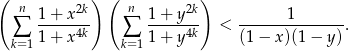
Każdy kąt trójkąta 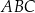 ma miarę mniejszą niż
ma miarę mniejszą niż 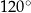 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 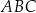 istnieje punkt
istnieje punkt 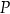 taki, że
taki, że
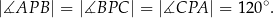
Magda napisała ciąg liczb, w którym każda liczba, począwszy od trzeciej, była sumą dwóch liczb ją poprzedzających. Czwartą liczbą w tym ciągu była liczba 6, a szóstą 15. Ile była równa siódma liczba w tym ciągu?
A) 9 B) 16 C) 21 D) 22 E) 24
Tomek urodził się w dniu 20 urodzin swojej matki, i potem oboje obchodzili równocześnie swoje urodziny. Ile razy wiek Tomka, liczony w dniu jego urodzin, będzie dzielnikiem wieku jego matki?
A) 4 B) 5 C) 6 D) 7 E) 8
Wyznacz najmniejszą liczbę 4-cyfrową, która przy dzieleniu przez 7 daje resztę 6, a przy dzieleniu przez 6 daje resztę 5.
Podstawy trapezu 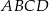 mają długości
mają długości 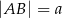 i
i 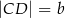 , przy czym
, przy czym 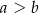 . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość
. Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość 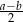 .
.
Wyznacz wszystkie pary liczb całkowitych dodatnich 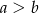 , dla których
, dla których
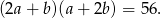
Oblicz pole rombu 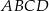 , wiedząc, że długości promieni okręgów opisanych na trójkątach
, wiedząc, że długości promieni okręgów opisanych na trójkątach 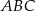 i
i 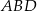 odpowiednio są równe
odpowiednio są równe 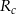 i
i 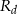 .
.
Rysunek obok przedstawia kwadratową płytkę. Narysowane na niej linie krzywe są ćwiartkami okręgów o promieniu równym połowie boku płytki. Długość takiej ćwiartki jest równa 5 dm. Z szesnastu takich płytek budujemy kwadrat. Jaką maksymalną długość może mieć nieprzerwana linia utworzona z ćwiartek tych okręgów?

A) 75 dm B) 100 dm C) 105 dm D) 110 dm E) 80 dm
Na płaszczyźnie wprowadzono układ współrzędnych. W początku układu współrzędnych siedzi kangur, który może wykonywać tylko skoki długości 1, przy czym każdy skok jest równoległy do którejś z osi układu. Ile jest punktów płaszczyzny, w których może znaleźć się kangur po wykonaniu dziesięciu skoków?
A) 121 B) 100 C) 400 D) 441 E) Inna liczba
Ile liczb sześciocyfrowych posiada tę własność, że każda ich cyfra, zaczynając od trzeciej, jest sumą dwóch poprzednich cyfr (cyfry liczymy od lewej strony)?
A) 1 B) 2 C) 3 D) 4 E) 6
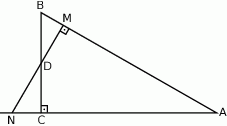
Przez środek 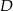 przyprostokątnej
przyprostokątnej 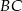 trójkąta prostokątnego
trójkąta prostokątnego 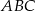 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 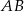 . Prosta ta przecina proste
. Prosta ta przecina proste 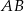 i
i 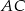 odpowiednio w punktach
odpowiednio w punktach 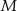 i
i 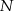 . Wykaż, że
. Wykaż, że 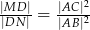 .
.
W kartonie znajdują się dwukolorowe piłeczki: 15 czerwono-niebieskich, 12 niebiesko-zielonych i 9 zielono-czerwonych. Przy jakiej najmniejszej liczbie piłeczek wybranych losowo z kartonu mamy gwarancję, że na co najmniej siedmiu z nich widnieje ten sam kolor?
A) 7 B) 8 C) 9 D) 10 E) 11
Śmigło wiatraka obraca się ze stałą prędkością, wykonując jeden pełny obrót w czasie 50 sekund. Ile płatów ma to śmigło, jeżeli fotokomórka umieszczona na szczycie tego wiatraka odnotowuje przesunięcie się płata co 10 sekund?
A) 2 B) 3 C) 5 D) 10 E) 50
Mecz koszykówki został rozstrzygnięty w dogrywce. W meczu tym najlepszy z zawodników zdobył 31 punktów. W każdej z kolejnych czterech kwart zdobywał więcej punktów niż w poprzedniej, a najwięcej w dogrywce. W dogrywce zawodnik ten zdobył 3 razy więcej punktów niż w pierwszej kwarcie. Ile punktów zdobył ten zawodnik w czwartej kwarcie?
A) 7 B) 10 C) 9 D) 6 E) 8
W karczmie jest 30 litrowa beczka wina napełniona do pełna. Winiarz zaczerpnął 1 litr wina i dolał do beczki 1 litr wody. Postąpił tak 10 razy. Ile czystego wina zostało w beczce.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 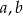 prawdziwa jest nierówność
prawdziwa jest nierówność
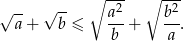
Jaką częścią największego kwadratu jest obszar zacieniowany?
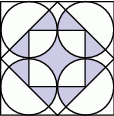
A) 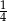 B)
B) 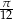 C)
C) 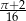 D)
D) 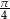 E)
E)