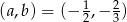Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 9977409

Wyznacz wszystkie wartości parametrów 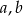a,b , dla których nierówność

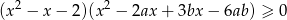
2 2 (x − x − 2)(x − 2ax + 3bx − 6ab) ≥ 0

jest spełniona przez każdą liczbę rzeczywistą.

Wersja PDF
Rozwiązanie

Rozkładamy pierwszy trójmian na czynniki.

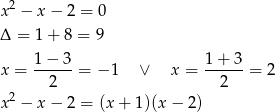
2 x − x − 2 = 0 Δ = 1 + 8 = 9 1− 3 1 + 3 x = ------= − 1 ∨ x = ------= 2 2 2 x2 − x − 2 = (x+ 1)(x− 2)

Teraz rozkładamy drugi trójmian

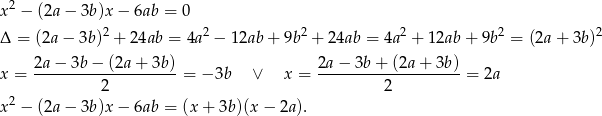
x2 − (2a − 3b)x − 6ab = 0 2 2 2 2 2 2 Δ = (2a− 3b) + 24ab = 4a − 12ab + 9b + 24ab = 4a + 12ab + 9b = (2a + 3b) 2a − 3b− (2a+ 3b) 2a − 3b + (2a + 3b ) x = -------------------- = − 3b ∨ x = --------------------= 2a 2 2 2 x − (2a − 3b)x − 6ab = (x+ 3b)(x − 2a).

Daną nierówność możemy więc zapisać w postaci

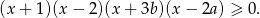
(x + 1)(x − 2)(x + 3b )(x− 2a) ≥ 0.

Jeżeli nierówność ma być spełniona przez każdą liczbę rzeczywistą to każdy pierwiastek lewej strony musi być podwójny, co daje nam dwie możliwości

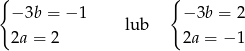
{ { − 3b = − 1 lub − 3b = 2 2a = 2 2a = − 1

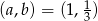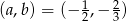Mamy zatem (a,b) = (1, 1) 3 lub (a,b) = (− 1,− 2) 2 3 .  
Odpowiedź: 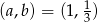1 (a,b) = (1 ,3) lub 1 2 (a,b) = (− 2,− 3)

Wersja PDF
lRozwiązaniellLosuj ponowniel