Zadanie nr 2138828
Uzasadnij, że równanie 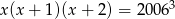 nie ma pierwiastków całkowitych.
nie ma pierwiastków całkowitych.
Rozwiązanie
Zauważmy, że jeżeli  jest liczbą całkowitą, to lewa strona równania jest iloczynem trzech kolejnych liczb całkowitych. Wśród trzech kolejnych liczb całkowitych zawsze jest liczba podzielna przez 3. Tymczasem prawa strona nie dzieli się przez 3, co oznacza, że równanie to nie może mieć rozwiązań całkowitych.
jest liczbą całkowitą, to lewa strona równania jest iloczynem trzech kolejnych liczb całkowitych. Wśród trzech kolejnych liczb całkowitych zawsze jest liczba podzielna przez 3. Tymczasem prawa strona nie dzieli się przez 3, co oznacza, że równanie to nie może mieć rozwiązań całkowitych.

