Zadanie nr 2342429
Określ liczbę rozwiązań równania 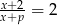 w zależności od wartości parametru
w zależności od wartości parametru 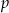 .
.
Rozwiązanie
Przekształćmy podane równanie (mnożymy przez mianownik).
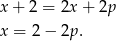
Na pierwszy rzut oka może się wydawać, że równanie ma zawsze jedno rozwiązanie, ale jest jeden haczyk. Trzeba pamiętać o tym, że w wyjściowym równaniu było 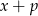 w mianowniku, zatem
w mianowniku, zatem 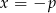 nie może być pierwiastkiem równania. Sprawdźmy kiedy tak jest.
nie może być pierwiastkiem równania. Sprawdźmy kiedy tak jest.
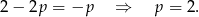
Zatem dla 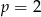 równanie nie ma rozwiązań.
równanie nie ma rozwiązań.
Odpowiedź: Jedno rozwiązanie dla 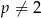 , brak rozwiązań dla
, brak rozwiązań dla 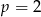 .
.

