/Szkoła średnia/Geometria/Planimetria/Różne

Zadanie nr 2618745

Podział odcinka, w wyniku którego otrzymujemy dwa odcinki takie, że stosunek długości krótszego z nich do długości dłuższego jest równy stosunkowi długości dłuższego odcinka do długości wyjściowego odcinka, nazywamy złotym podziałem odcinka.

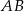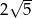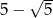  • Odcinek AB podzielono na dwa odcinki o długościach √ -- 2 5 i √ -- 5− 5 . Rozstrzygnij, czy dokonano złotego podziału odcinka AB .
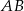  • Dokonano złotego podziału odcinka o długości 2. Oblicz długości odcinków, na jakie podzielono dany odcinek.
Wersja PDF

Rozwiązanie

  • Ponieważ
    √ -- √ -- 2 5 > 5− 5

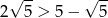
    musimy sprawdzić, czy

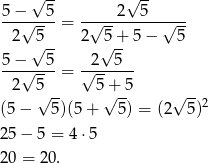
    √ -- √ -- 5-−---5- -----2--5------ 2√ 5 = 2√ 5 + 5 − √ 5 √ -- √ -- 5-−√--5-= √-2--5-- 2 5 5 + 5 √ -- √ -- √ --2 (5 − 5)(5 + 5) = (2 5) 25 − 5 = 4⋅5 20 = 20.

    Zatem jest jest to złoty podział odcinka.  
    Odpowiedź: Tak, dokonano.

  • Niech x będzie długością krótszej części. Mamy wtedy równanie
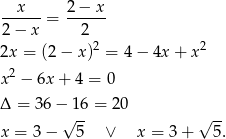
    x 2 − x ------= ------ 2 − x 2 2x = (2− x)2 = 4 − 4x + x2 2 x − 6x + 4 = 0 Δ = 36 − 16 = 2 0 √ -- √ -- x = 3− 5 ∨ x = 3 + 5.

    Odrzucamy rozwiązanie większe od 2 i otrzymujemy

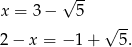
    √ -- x = 3 − 5 √ -- 2− x = − 1+ 5.

     
    Odpowiedź: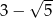 √ -- 3 − 5 i √ -- 5 − 1

Wersja PDF
Rozwiązanie Losuj ponownie