/Szkoła średnia/Ciągi/Szereg geometryczny/Na dowodzenie

Zadanie nr 9241438

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest nieskończony ciąg geometryczny 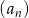(an) , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 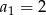a1 = 2 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 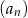(an ) jest równa sumie kwadratów wszystkich wyrazów tego ciągu.

Rozwiązanie

Oznaczmy przez 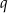q iloraz danego ciągu – ponieważ ciąg zawiera wyrazy różnych znaków mamy oczywiście 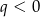q < 0 . Z podanej informacji o ciągu arytmetycznym mamy

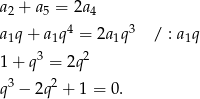
a2 + a5 = 2a 4 4 3 a1q + a1q = 2a1q / : a 1q 1 + q3 = 2q 2 3 2 q − 2q + 1 = 0 .

Widać, że jednym z pierwiastków powyższego równania jest 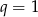q = 1 . Aby wyznaczyć pozostałe pierwiastki, dzielimy ten wielomian przez 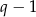q− 1 – my jak zwykle zrobimy to grupując wyrazy.

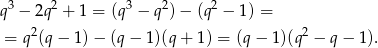
q3 − 2q2 + 1 = (q3 − q2) − (q2 − 1) = 2 2 = q (q − 1) − (q − 1)(q + 1) = (q − 1)(q − q − 1).

Rozkładamy trójmian w drugim nawiasie.

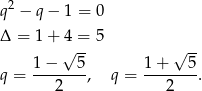
2 q − q − 1 = 0 Δ = 1 + 4 = 5 √ -- √ -- 1−----5- 1+----5- q = 2 , q = 2 .

Ustaliliśmy wcześniej, że 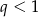q < 1 , więc drugi pierwiastek odrzucamy i mamy

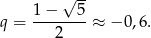
√ -- q = 1-−---5-≈ − 0,6. 2

To oznacza, że szereg geometryczny odpowiadający ciągowi 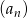(an ) jest zbieżny (tzn. suma wyrazów ciągu 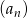(an ) jest skończona).

Spróbujmy teraz zastanowić się nad tym, co mamy udowodnić. Ciąg sześcianów wyrazów ciągu 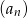(an) , czyli ciąg 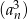3 (an ) jest też ciągiem geometrycznym, ale o ilorazie 3 q .

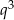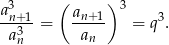
3 ( ) 3 an+1-= an+-1 = q3. a3n an

Podobnie ciąg kwadratów 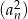(a2n) jest ciągiem geometrycznym o ilorazie 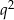q2 . Mamy więc udowodnić, że

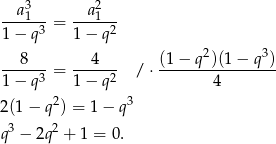
a31 a21 -----3-= -----2- 1 − q 1 − q ---8--- --4---- (1−--q2)(1−--q3) 1 − q3 = 1 − q2 / ⋅ 4 2(1 − q2) = 1 − q3 3 2 q − 2q + 1 = 0.

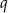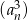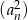Wystarczy teraz zauważyć, że powyższe równanie to to samo równanie, z którego obliczyliśmy q . To oznacza, że rzeczywiście suma wyrazów ciągu (a3n) jest równa sumie wyrazów ciągu (a2n) .

Wersja PDF
Rozwiązanie Losuj ponownie