/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Trzy okręgi styczne

Zadanie nr 2477905

Każde dwa spośród trzech okręgów są zewnętrznie styczne. Oblicz promienie tych okręgów, jeśli wiadomo, że odległości między ich środkami wynoszą 8, 11, 13.

Rozwiązanie

Zacznijmy od rysunku.

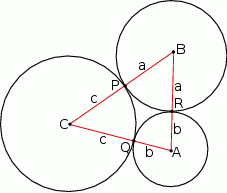
Jeżeli oznaczymy długości promieni trzech danych okręgów przez 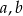a,b i , to z podanych odległości między ich środkami otrzymujemy układ równań.

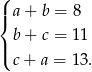
( | a + b = 8 { | b + c = 11 ( c + a = 13.

Dodając pierwsze dwa równania stronami mamy

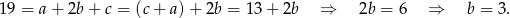
19 = a + 2b + c = (c+ a) + 2b = 13+ 2b ⇒ 2b = 6 ⇒ b = 3.

Stąd

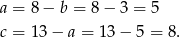
a = 8− b = 8 − 3 = 5 c = 13 − a = 13 − 5 = 8.

Odpowiedź: 3, 5 i 8

Wersja PDF