Zadanie nr 8479311
Uzasadnij, że suma kwadratów dwóch kolejnych nieparzystych liczb całkowitych nie może być kwadratem liczby całkowitej.
Rozwiązanie
Jeżeli oznaczymy te dwie liczby przez 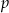 i
i 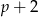 , gdzie
, gdzie 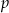 jest liczbą nieparzystą, to suma kwadratów jest równa
jest liczbą nieparzystą, to suma kwadratów jest równa
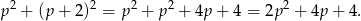
Teraz wystarczy zauważyć, że liczba ta dzieli się przez dwa, ale nie dzieli się przez 4 (bo 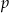 jest liczbą nieparzystą). Nie może to więc być kwadrat liczby całkowitej (bo kwadrat liczby nieparzystej nie dzieli się przez 2, a kwadrat liczby parzystej dzieli się przez 4).
jest liczbą nieparzystą). Nie może to więc być kwadrat liczby całkowitej (bo kwadrat liczby nieparzystej nie dzieli się przez 2, a kwadrat liczby parzystej dzieli się przez 4).

