Zadanie nr 6242955
Porównaj liczby 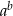 i
i 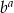 , gdzie
, gdzie ![[ √ --1 √ --1]2 a = (2− 3)2 + (2+ 3)2](https://img.zadania.info/zad/6242955/HzadT2x.gif) ,
, 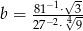 .
.
Rozwiązanie
Liczymy
![[ √ --1]2 √ --1 √ -- 1 [ √ --1]2 a = (2− 3)2 + 2(2 − 3)2(2 + 3 )2 + (2+ 3)2 = [ ] 1 √ -- √ -- √ -- 2 √ -- = 2− 3+ 2 (2 − 3)(2 + 3) + 2+ 3 = 12 = 4+ 2[4 − 3 ] = 4+ 2 = 6](https://img.zadania.info/zad/6242955/HzadR0x.gif)
Teraz pora na 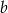 .
.
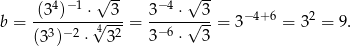
Liczby 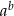 i
i 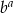 są dość duże, więc policzmy ich iloraz (skróci się wspólna potęga 3).
są dość duże, więc policzmy ich iloraz (skróci się wspólna potęga 3).
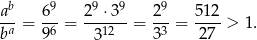
Zatem 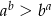 .
.
Odpowiedź: 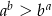
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Porównaj liczby 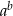 i
i 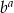 , gdzie
, gdzie ![[ √ --1 √ --1]2 a = (2− 3)2 + (2+ 3)2](https://img.zadania.info/zad/6242955/HzadT2x.gif) ,
, 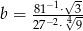 .
.
Liczymy
![[ √ --1]2 √ --1 √ -- 1 [ √ --1]2 a = (2− 3)2 + 2(2 − 3)2(2 + 3 )2 + (2+ 3)2 = [ ] 1 √ -- √ -- √ -- 2 √ -- = 2− 3+ 2 (2 − 3)(2 + 3) + 2+ 3 = 12 = 4+ 2[4 − 3 ] = 4+ 2 = 6](https://img.zadania.info/zad/6242955/HzadR0x.gif)
Teraz pora na 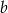 .
.
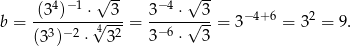
Liczby 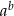 i
i 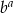 są dość duże, więc policzmy ich iloraz (skróci się wspólna potęga 3).
są dość duże, więc policzmy ich iloraz (skróci się wspólna potęga 3).
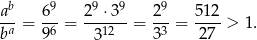
Zatem 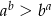 .
.
Odpowiedź: