Punkt 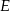 jest środkiem boku
jest środkiem boku 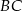 prostokąta
prostokąta 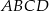 , w którym
, w którym 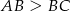 . Punkt
. Punkt 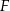 leży na boku
leży na boku 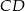 tego prostokąta oraz
tego prostokąta oraz 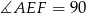 . Udowodnij, że
. Udowodnij, że 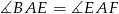 .
.
/Konkursy/Zadania/Geometria/Planimetria/Prostokąt/Różne
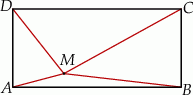
Punkt 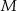 leży wewnątrz prostokąta
leży wewnątrz prostokąta 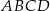 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 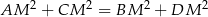 .
.
Oblicz jakie długości powinny mieć boki prostokąta o polu równym 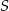 , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
, aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
Dany jest prostokąt 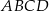 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 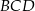 jest styczny do przekątnej
jest styczny do przekątnej 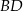 w punkcie
w punkcie 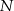 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 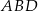 jest styczny do boku
jest styczny do boku 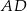 w punkcie
w punkcie 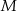 , a środek
, a środek 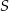 tego okręgu leży na odcinku
tego okręgu leży na odcinku 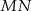 , jak na rysunku.
, jak na rysunku.
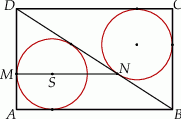
Wykaż, że 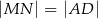 .
.
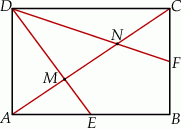
W prostokącie 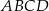 wierzchołek
wierzchołek 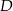 połączono odcinkami ze środkami
połączono odcinkami ze środkami 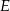 i
i 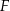 boków
boków 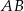 i
i 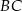 , zaś
, zaś 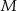 i
i 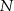 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 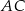 .
.
- Uzasadnij, że odcinki
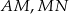 i
i 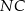 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
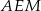 i
i 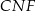 mają równe pola.
mają równe pola.
Na bokach 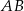 i
i 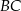 prostokąta
prostokąta 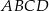 wybrano punkty
wybrano punkty 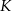 i
i 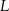 w ten sposób, że trójkąt
w ten sposób, że trójkąt 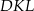 jest ostrokątny oraz
jest ostrokątny oraz 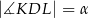 . Odcinek
. Odcinek 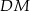 jest wysokością trójkąta
jest wysokością trójkąta 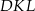 .
.
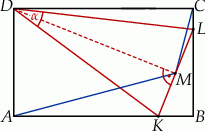
Wykaż, że 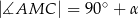 .
.
Punkt 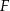 jest środkiem boku
jest środkiem boku 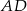 prostokąta
prostokąta 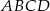 , w którym
, w którym 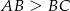 . Punkt
. Punkt 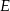 jest takim punktem boku
jest takim punktem boku 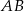 tego prostokąta, że prosta
tego prostokąta, że prosta 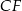 jest dwusieczną kąta
jest dwusieczną kąta 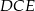 . Wykaż, że trójkąt
. Wykaż, że trójkąt 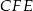 jest prostokątny.
jest prostokątny.
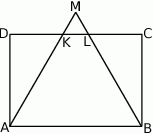
Dany jest prostokąt 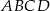 , w którym
, w którym 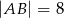 i
i 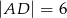 . Na boku
. Na boku 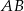 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 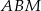 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta 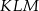 .
.