Oblicz całkę 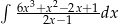 .
.
/Studia/Analiza
Rozważamy wszystkie proste na płaszczyźnie, które są jednocześnie styczne do wykresu funkcji homograficznej 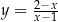 oraz do okręgu o równaniu
oraz do okręgu o równaniu 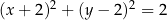 . Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
. Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
Oblicz całkę niewłaściwą 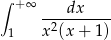
Wyznaczyć obrazy zbiorów 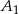 i
i 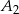 oraz przeciwobraz zbioru
oraz przeciwobraz zbioru 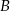 przy funkcji
przy funkcji 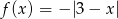 , jeżeli
, jeżeli ![A1 = [− 2,3), A 2 = (− 2,5], B = (− ∞ ,− 3]∪ {0}](https://img.zadania.info/zad/5457974/HzadT4x.gif) .
.
Oblicz granicę 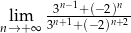 .
.
Oblicz całkę 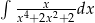 .
.
Zbadaj monotoniczność ciągu 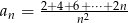 .
.
Oblicz granicę 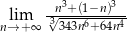 .
.
Oblicz całkę 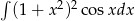 .
.
Oblicz granicę 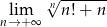 .
.
Wykaż, że funkcja 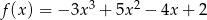 nie ma ekstremum.
nie ma ekstremum.
Oblicz całkę 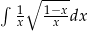 .
.
Oblicz całkę 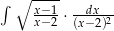 .
.
Oblicz całkę 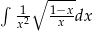 .
.
Oblicz pochodną funkcji 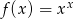 .
.
Oblicz granicę 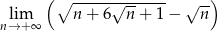 .
.
Oblicz granicę 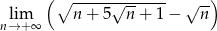 .
.
Oblicz granicę 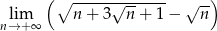 .
.
Oblicz granicę 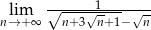 .
.
Oblicz granicę 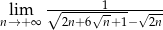 .
.
Oblicz granicę 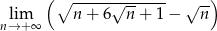 .
.
Oblicz granicę 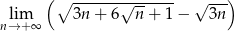 .
.
Oblicz granicę 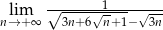 .
.
Oblicz granicę 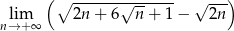 .
.
Oblicz granicę 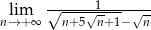 .
.
Zbadaj monotoniczność ciągu danego wzorem 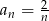 .
.
Oblicz całkę niewłaściwą 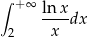 .
.
Oblicz pole trójkąta utworzonego przez prostą 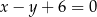 , oś
, oś 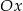 oraz styczną do wykresu funkcji
oraz styczną do wykresu funkcji 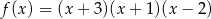 w punkcie o pierwszej współrzędnej
w punkcie o pierwszej współrzędnej 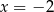 .
.
Wyznacz wszystkie proste, które są jednocześnie styczne do paraboli 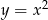 oraz okręgu o równaniu
oraz okręgu o równaniu 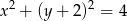 .
.
Oblicz z definicji pochodną funkcji 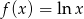 .
.
Wyznacz te wartości  , dla których ciąg geometryczny
, dla których ciąg geometryczny 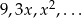 jest zbieżny.
jest zbieżny.

