Stosunek długości ramion trapezu opisanego na okręgu o promieniu 6 cm wynosi 3:4. Obwód trapezu jest równy 70 cm. Oblicz długości podstaw trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny opisany na okręgu
W trapez 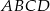 , gdzie
, gdzie 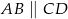 i
i 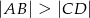 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
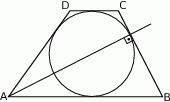
Dwusieczna kąta ostrego przy wierzchołku 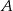 jest prostopadła do ramienia
jest prostopadła do ramienia 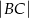 .
.
- Wykaż, że dwusieczna kąta przy wierzchołku
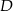 jest równoległa do ramienia
jest równoległa do ramienia 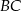 .
. - Oblicz
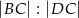 .
.
Ramiona trapezu opisanego na okręgu mają długości 3 cm i 5 cm. Odcinek łączący środki ramion dzieli trapez na dwie figury, których stosunek pól wynosi 5:11. Oblicz długości podstaw trapezu.
W trapezie opisanym na okręgu ramiona mają długości 6 i 10. Odcinek łączący środki tych ramion dzieli trapez na dwie części, których pola pozostają w stosunku 5:11. Wyznacz długości podstaw tego trapezu.
W trapezie opisanym na okręgu boki nierównoległe mają długości 3 i 5, zaś odcinek łączący środki tych boków dzieli trapez na dwie części, których pola są w stosunku 5:11. Oblicz długości podstaw trapezu.
Na okręgu o promieniu 8 cm opisano trapez. Kąty, które tworzą ramiona z dłuższą podstawą mają miarę 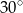 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Na okręgu o promieniu  opisano trapez, w którym
opisano trapez, w którym 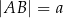 i
i 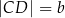 .
.
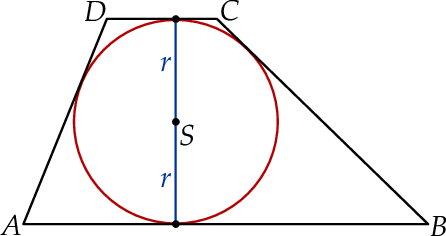
Wykaż, że 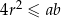 .
.
Na okręgu opisano trapez, w którym krótsza podstawa ma długość  , a dłuższa podstawa tworzy z ramionami kąty o mierze
, a dłuższa podstawa tworzy z ramionami kąty o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapezie 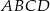 ramiona mają długości
ramiona mają długości 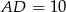 oraz
oraz 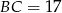 , zaś tangens kąta nachylenia ramienia
, zaś tangens kąta nachylenia ramienia 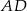 do dłuższej podstawy
do dłuższej podstawy 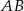 wynosi
wynosi 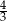 . Wiedząc, że w dany trapez można wpisać okrąg oblicz
. Wiedząc, że w dany trapez można wpisać okrąg oblicz
- pole trapezu,
- pole trójkąta
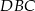 .
.
W trapez 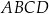 wpisano okrąg o środku
wpisano okrąg o środku 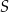 . Okrąg ten jest styczny do ramion
. Okrąg ten jest styczny do ramion 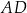 i
i 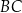 tego trapezu w punktach odpowiednio
tego trapezu w punktach odpowiednio 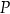 i
i 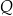 (zobacz rysunek).
(zobacz rysunek).

Uzasadnij, że trójkąt 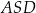 jest prostokątny. Wykaż, że
jest prostokątny. Wykaż, że 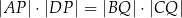 .
.
W trapezie opisanym na okręgu kąty przy dłuższej podstawie mają miary 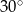 i
i 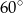 , a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.
, a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.
Punkt 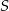 jest środkiem okręgu wpisanego w trapez
jest środkiem okręgu wpisanego w trapez 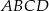 (
(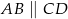 ). Wykaż, że trójkąt
). Wykaż, że trójkąt 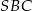 jest prostokątny.
jest prostokątny.
Dany jest trapez opisany na okręgu, którego kąty przy jednej podstawie są ostre, oraz którego pole jest równe 168. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów jeżeli ramiona trapezu mają długości 13 i 15.
W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.
Kąty ostre trapezu opisanego na okręgu mają miary  i
i 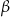 , a pole tego trapezu jest równe
, a pole tego trapezu jest równe 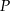 . Oblicz długość promienia okręgu wpisanego w ten trapez.
. Oblicz długość promienia okręgu wpisanego w ten trapez.

