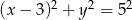Zadanie nr 5210178
Napisz równanie okręgu, którego środek znajduje się na prostej 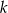 , przechodzącego przez punkty
, przechodzącego przez punkty 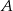 i
i 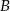 , jeśli
, jeśli 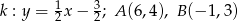 .
.
Rozwiązanie
Zaczynamy od rysunku.
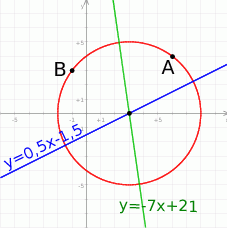
Środek okręgu wyznaczymy pisząc równanie symetralnej odcinka 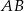 i znajdując jej punkt wspólny z prostą
i znajdując jej punkt wspólny z prostą 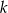 .
.
Symetralną odcinka 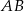 wyznaczymy korzystając ze wzoru na równanie prostej prostopadłej do wektora
wyznaczymy korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/5210178/HzadR4x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 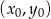
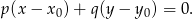
W naszej sytuacji mamy wektor ![→ AB = [− 7,− 1]](https://img.zadania.info/zad/5210178/HzadR7x.gif) i punkt
i punkt 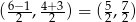 . Zatem symetralna odcinka
. Zatem symetralna odcinka 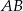 ma równanie
ma równanie
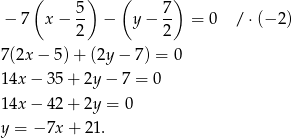
Korzystamy teraz z równania prostej 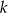 :
:
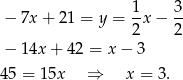
Zatem 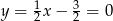 i
i 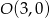 . Pozostało wyliczyć promień
. Pozostało wyliczyć promień
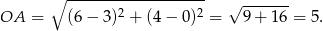
Zatem okrąg ma równanie
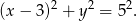
Odpowiedź: