Funkcja 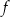 jest określona wzorem
jest określona wzorem 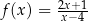 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 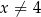 . W kartezjańskim układzie współrzędnych
. W kartezjańskim układzie współrzędnych 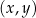 punkt
punkt 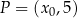 należy do wykresu funkcji
należy do wykresu funkcji 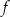 . Oblicz
. Oblicz 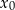 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 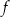 w punkcie
w punkcie 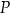 .
.
/Studia/Analiza/Funkcje
Oblicz z definicji pochodną funkcji 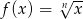 , gdzie
, gdzie 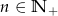 .
.
Wyznacz asymptoty funkcji 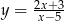 .
.
Znajdź wzór na sumę 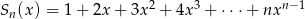 .
.
Uzasadnij, że funkcja 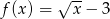 jest różnowartościowa na zbiorze
jest różnowartościowa na zbiorze 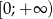 .
.
Oblicz granicę funkcji 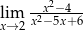 .
.
Oblicz granicę funkcji 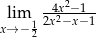 .
.
Oblicz miarę kąta ostrego pod jakim przecinają się styczne do wykresu funkcji
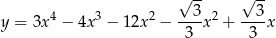
poprowadzone w punktach o pierwszych współrzędnych równych 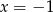 i
i 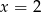 .
.
Oblicz miarę kąta ostrego pod jakim przecinają się styczne do wykresu funkcji
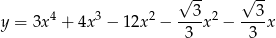
poprowadzone w punktach o pierwszych współrzędnych równych 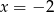 i
i 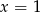 .
.
Zbadać, czy istnieje granica: 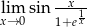 .
.
Uzasadnij, że funkcja 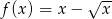 jest różnowartościowa na zbiorze
jest różnowartościowa na zbiorze 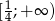 .
.
Wyznacz funkcję odwrotną do funkcji: 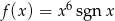 .
.
Oblicz granicę 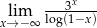 .
.
Oblicz granicę 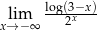 .
.
Udowodnij, że jeśli funkcje 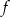 i
i 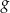 są nieparzyste, to funkcja
są nieparzyste, to funkcja 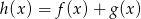 jest nieparzysta,
jest nieparzysta,
Udowodnij, że jeśli funkcje 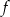 i
i 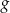 są nieparzyste, to funkcja
są nieparzyste, to funkcja 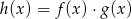 jest parzysta.
jest parzysta.
Dane są funkcje 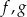 i
i 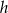 określone wzorami:
określone wzorami: 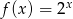 ,
, 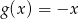 ,
, 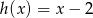 dla
dla 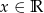 .
.
- Naszkicuj wykres funkcji
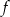 .
. - Wyznacz wzór i naszkicuj wykres funkcji
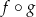 .
. - Wyznacz wzór i naszkicuj wykres funkcji
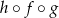 .
.
Oblicz pochodną funkcji 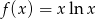 .
.
Oblicz granicę 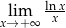 .
.
Napisz równanie stycznej do wykresu funkcji 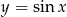 w punkcie
w punkcie 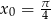 .
.
Naszkicuj wykres funkcji: 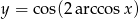 .
.
Wyznacz punkty wspólne wykresów 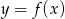 i
i 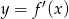 jeżeli
jeżeli 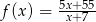 .
.
Wyznacz punkty wspólne wykresów 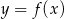 i
i 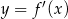 jeżeli
jeżeli 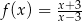 .
.
Oblicz pochodną funkcji 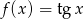 .
.
Oblicz pochodną funkcji 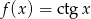 .
.
Wyznacz ekstrema lokalne funkcji 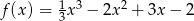 .
.

