/Studia/Algebra liniowa/Odwzorowania liniowe

Zadanie nr 1351090

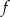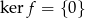Wykazać, że na to aby odwzorowanie było różnowartościowe potrzeba i wystarcza, aby ke rf = { 0} .

Rozwiązanie

„”
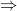Odwzorowanie liniowe spełnia warunek 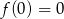f(0) = 0 , więc jeżeli odwzorowanie jest różnowartościowe, to do jądra należy tylko wektor zerowy (odwzorowanie nie może tej samej wartości przyjąć w dwóch różnych punktach).
„”
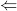Na odwrót, załóżmy, że 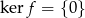k erf = { 0} i niech 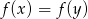f(x ) = f(y) . Wtedy, z liniowości

0 = f(x) − f(y) = f(x − y) ⇒ x − y ∈ k erf ⇒ x = y.

Wersja PDF