Udowodnij, że w trójkącie równoramiennym wysokości poprowadzone do równych boków są równej długości.
/Szkoła podstawowa/Geometria
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 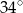 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 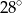 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 5 razy większa od miary drugiego.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 4 razy większa od miary drugiego.
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
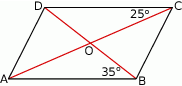
Oblicz miarę kąta rozwartego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
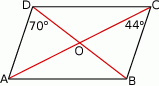
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
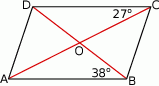
Objętość ostrosłupa prawidłowego czworokątnego jest równa 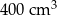 , a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
, a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
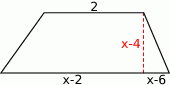
Pole trapezu przedstawionego na rysunku jest równe 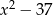 . Oblicz
. Oblicz  .
.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe 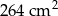 . Pole podstawy tej bryły stanowi 75% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 75% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe 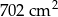 . Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
Na rysunku przedstawiono równoległobok 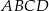 i trójkąt
i trójkąt 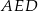 . Punkt
. Punkt 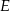 leży na odcinku
leży na odcinku 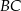 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 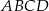 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta  .
.
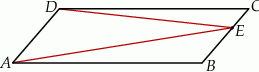
Okrąg o środku w punkcie 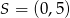 ma promień długości 1 i jest styczny do okręgu o środku
ma promień długości 1 i jest styczny do okręgu o środku 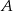 i promieniu długości 10. Punkt
i promieniu długości 10. Punkt 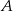 leży na osi
leży na osi 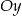 . Jakie ma współrzędne?
. Jakie ma współrzędne?
W trójkącie 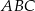 dwusieczna kąta przy wierzchołku
dwusieczna kąta przy wierzchołku 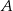 przecina symetralną boku
przecina symetralną boku 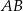 pod kątem
pod kątem 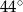 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 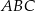 jest trójkątem rozwartokątnym.
jest trójkątem rozwartokątnym.
Oblicz pole sześciokąta foremnego o boku długości 2.
Oblicz obwód trójkąta o wierzchołkach: 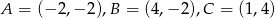 .
.
Oblicz obwód trójkąta o wierzchołkach: 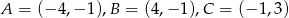 .
.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 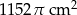 .
.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 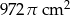 .
.
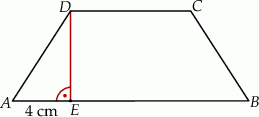
Trapez równoramienny 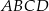 , którego pole jest równe
, którego pole jest równe 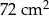 , podzielono na trójkąt
, podzielono na trójkąt 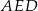 i trapez
i trapez 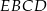 . Odcinek
. Odcinek 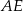 ma długość równą 4 cm, a odcinek
ma długość równą 4 cm, a odcinek 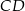 jest od niego 2 razy dłuższy. Oblicz pole trójkąta
jest od niego 2 razy dłuższy. Oblicz pole trójkąta 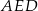 .
.
Dany jest równoległobok 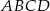 . Na przedłużeniu przekątnej
. Na przedłużeniu przekątnej 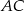 wybrano punkt
wybrano punkt 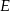 tak, że
tak, że 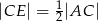 (zobacz rysunek). Uzasadnij, że pole równoległoboku
(zobacz rysunek). Uzasadnij, że pole równoległoboku 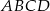 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 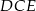 .
.
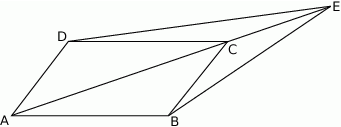
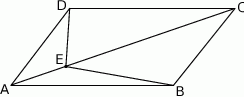
Na przekątnej 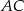 równoległoboku
równoległoboku 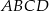 wybrano punkt
wybrano punkt 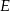 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 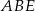 i
i 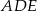 mają równe pola.
mają równe pola.
Oblicz obwód czworokąta o wierzchołkach: 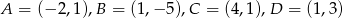 .
.
Obwód rombu wynosi 18 cm, a jego pole 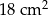 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
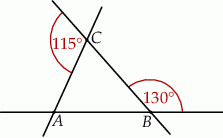
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt 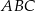 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 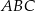 jest równoramienny.
jest równoramienny.
Cięciwa okręgu tworzy kąt 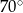 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Cięciwa okręgu tworzy kąt 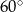 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Cięciwa okręgu tworzy kąt 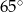 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 12. Wyznacz obwód każdego z tych trójkątów.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 18. Wyznacz obwód każdego z tych trójkątów.
Dany jest prostokąt 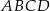 . Na boku
. Na boku 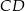 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 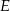 , że
, że 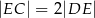 , a na boku
, a na boku 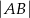 wybrano taki punkt
wybrano taki punkt 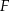 , że
, że 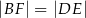 . Niech
. Niech 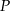 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 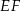 z prostą
z prostą 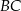 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 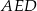 i
i 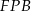 są przystające.
są przystające.
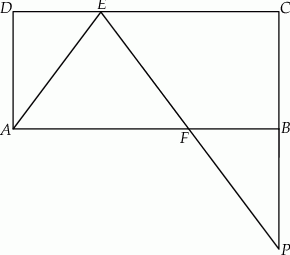
Dany jest prostokąt 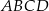 . Na boku
. Na boku 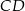 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 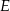 , że
, że 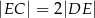 , a na przedłużeniu boku
, a na przedłużeniu boku 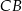 wybrano taki punkt
wybrano taki punkt 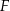 , że
, że 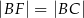 . Niech
. Niech 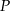 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 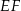 z prostą
z prostą 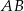 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 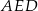 i
i 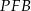 są przystające.
są przystające.