Cięciwa okręgu tworzy kąt 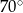 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
/Szkoła podstawowa/Geometria
Cięciwa okręgu tworzy kąt 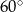 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Cięciwa okręgu tworzy kąt 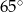 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 12. Wyznacz obwód każdego z tych trójkątów.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 18. Wyznacz obwód każdego z tych trójkątów.
Dany jest prostokąt 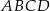 . Na boku
. Na boku 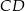 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 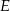 , że
, że 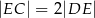 , a na boku
, a na boku 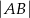 wybrano taki punkt
wybrano taki punkt 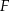 , że
, że 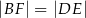 . Niech
. Niech 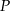 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 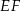 z prostą
z prostą 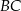 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 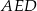 i
i 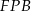 są przystające.
są przystające.
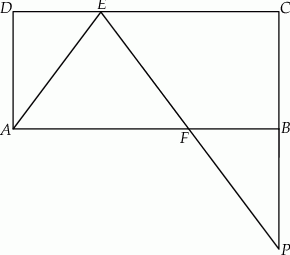
Dany jest prostokąt 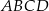 . Na boku
. Na boku 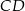 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 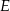 , że
, że 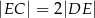 , a na przedłużeniu boku
, a na przedłużeniu boku 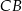 wybrano taki punkt
wybrano taki punkt 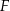 , że
, że 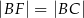 . Niech
. Niech 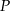 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 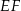 z prostą
z prostą 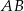 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 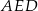 i
i 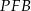 są przystające.
są przystające.
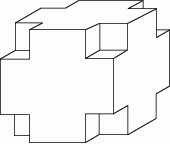
Z sześcianu zbudowanego z 64 małych sześcianów o krawędzi 1 cm usunięto z każdego narożnika po jednym małym sześcianie (patrz rysunek). Oblicz pole powierzchni powstałej bryły i porównaj je z polem powierzchni dużego sześcianu. Zapisz obliczenia.
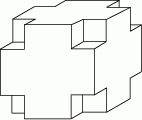
Z sześcianu zbudowanego z 125 małych sześcianów o krawędzi 1 cm usunięto z każdego narożnika po jednym małym sześcianie (patrz rysunek). Oblicz pole powierzchni powstałej bryły.
Przekątne prostokąta mają długość 20 cm i przecinają się pod kątem 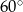 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
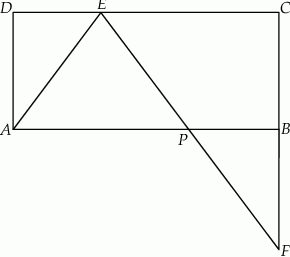
Prostokąt 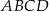 o wymiarach 7 cm i 8 cm rozcięto wzdłuż prostej
o wymiarach 7 cm i 8 cm rozcięto wzdłuż prostej  na dwa trapezy tak, jak pokazano na rysunku. Odcinek
na dwa trapezy tak, jak pokazano na rysunku. Odcinek 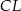 ma długość 3,2 cm.
ma długość 3,2 cm.
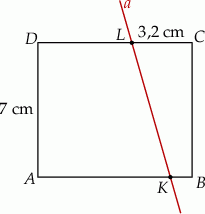
Pole trapezu 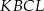 jest czterokrotnie mniejsze od pola prostokąta
jest czterokrotnie mniejsze od pola prostokąta 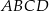 . Oblicz długość odcinka
. Oblicz długość odcinka 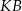 . Zapisz obliczenia.
. Zapisz obliczenia.
Oblicz miarę kąta 
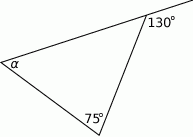
Oblicz miarę kąta 
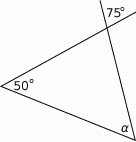
Oblicz miarę kąta 
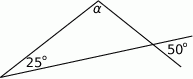
Oblicz miarę kąta 
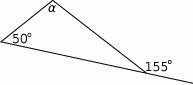
Oblicz miarę kąta 
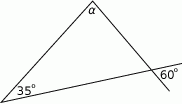
Oblicz miarę kąta 
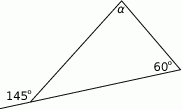
Oblicz obwód okręgu wpisanego w kwadrat, którego bok ma długość 10cm.
Podstawa ostrosłupa prawidłowego czworokątnego ma pole 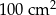 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 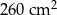 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W prostokącie 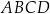 bok
bok 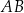 jest cztery razy dłuższy od boku
jest cztery razy dłuższy od boku 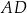 . Punkty
. Punkty 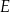 i
i 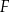 dzielą odcinek
dzielą odcinek 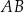 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
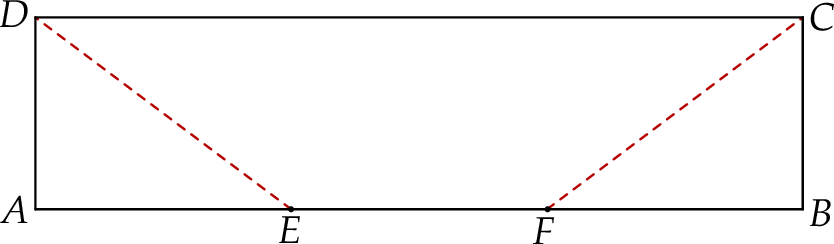
Oblicz pole trapezu 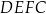 jeżeli wiadomo, że jego obwód jest równy 52 cm.
jeżeli wiadomo, że jego obwód jest równy 52 cm.
Punkty 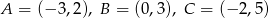 to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta
to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta 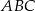 względem
względem
- osi
 ,
, - osi
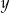 ,
, - punktu
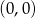 .
.
Prostokąt o obwodzie 48 cm rozcięto na dwa jednakowe prostokąty, każdy o obwodzie 39 cm. Jakie wymiary miał prostokąt przed rozcięciem?
Podstawą ostrosłupa o wysokości 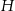 jest kwadrat. Na rysunku przedstawiono siatkę i podano długości niektórych krawędzi tego ostrosłupa.
jest kwadrat. Na rysunku przedstawiono siatkę i podano długości niektórych krawędzi tego ostrosłupa.
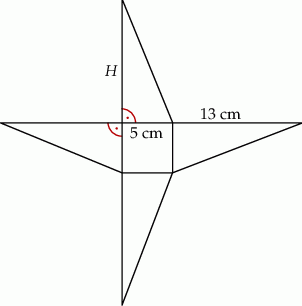
Oblicz objętość tego ostrosłupa.
Oblicz średnicę koła o polu 1.
Oblicz średnicę koła o polu 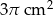 .
.
Oblicz średnicę koła o polu 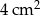 .
.
Oblicz średnicę koła o polu 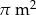 .
.
Oblicz miarę kąta  .
.
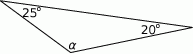
Oblicz miarę kąta  .
.

Oblicz miarę kąta  .
.

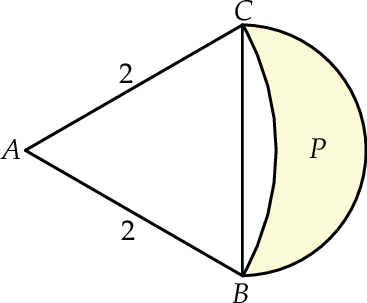
Trójkąt 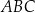 jest trójkątem równobocznym o boku długości 2. Obszar
jest trójkątem równobocznym o boku długości 2. Obszar 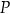 jest zawarty między półokręgiem o średnicy
jest zawarty między półokręgiem o średnicy 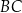 i łukiem okręgu o środku
i łukiem okręgu o środku 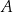 przechodzącym przez punkty
przechodzącym przez punkty 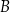 i
i 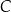 . Oblicz pole obszaru
. Oblicz pole obszaru 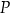 .
.
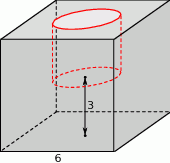
W sześcianie o krawędzi podstawy 6 wydrążono pionowy walec, którego wysokość i średnica są równe połowie długości krawędzi sześcianu. Oblicz pole powierzchni całkowitej tej bryły.
Ile ścian bocznych ma graniastosłup o 14 wierzchołkach?
Czy istnieje graniastosłup, który nie ma przekątnych?
Czy graniastosłup może mieć 20 krawędzi?
Czy w każdym graniastosłupie prawidłowym wszystkie przekątne mają tę samą długość?
Czy graniastosłup może mieć 10 ścian bocznych i 20 wierzchołków?
Ile ścian bocznych ma graniastosłup o 100 wierzchołkach?
Dwusieczna kąta ostrego 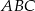 przecina przyprostokątną
przecina przyprostokątną 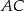 trójkąta prostokątnego
trójkąta prostokątnego 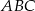 w punkcie
w punkcie  .
.
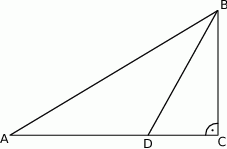
Udowodnij, że jeżeli 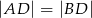 , to
, to 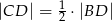 .
.
Dwusieczna kąta ostrego 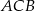 przecina przyprostokątną
przecina przyprostokątną 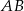 trójkąta prostokątnego
trójkąta prostokątnego 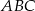 w punkcie
w punkcie 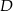 .
.
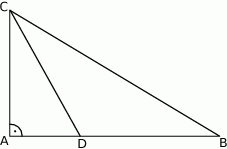
Udowodnij, że jeżeli 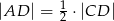 , to
, to 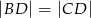 .
.
Agata postanowiła przygotować kartkę okolicznościową w kształcie prostokąta, ozdobioną wzorem dokładnie takim, jak przedstawiony na rysunku. Kartka ta będzie miała wymiary 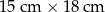 . Do jej ozdobienia Agata chce użyć jednakowych kwadratów, których bok wyraża się całkowitą liczbą centymetrów. Niektóre z tych kwadratów będzie musiała przeciąć na dwie lub na cztery jednakowe części.
. Do jej ozdobienia Agata chce użyć jednakowych kwadratów, których bok wyraża się całkowitą liczbą centymetrów. Niektóre z tych kwadratów będzie musiała przeciąć na dwie lub na cztery jednakowe części.
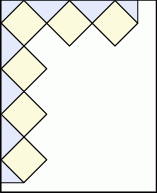
Oblicz maksymalną długość boku jednego kwadratu. Do obliczeń przyjmij przybliżenie 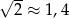 .
.
Karol przykleja na kartce formatu A4 (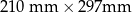 ) kwadraty o boku 2 cm, według wzoru, którego fragment pokazano na rysunku.
) kwadraty o boku 2 cm, według wzoru, którego fragment pokazano na rysunku.
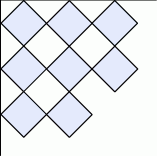
Przekątne każdego kwadratu są równoległe do krawędzi kartki i kwadraty stykają się jednym wierzchołkiem. Oblicz ile maksymalnie takich kwadratów Karol będzie mógł przykleić na kartce. Do obliczeń przyjmij przybliżenie 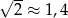 .
.

