Na rysunku przedstawiono prostokąt 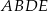 i trójkąt
i trójkąt 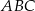 . Punkty
. Punkty 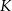 i
i 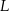 dzielą odcinki
dzielą odcinki 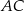 i
i 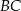 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 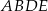 jest równe polu trójkąta
jest równe polu trójkąta 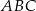 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono prostokąt 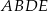 i trójkąt
i trójkąt 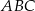 . Punkty
. Punkty 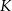 i
i 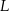 dzielą odcinki
dzielą odcinki 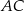 i
i 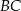 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 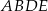 jest równe polu trójkąta
jest równe polu trójkąta 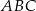 .
.

Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
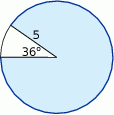
Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
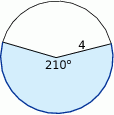
Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
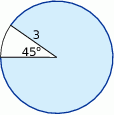
Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
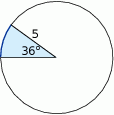
Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
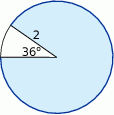
Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
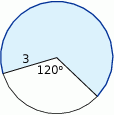
Oblicz długość łuku ograniczającego zacieniowany wycinka koła.
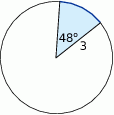
Boki trójkąta mają długości 13 cm, 20 cm i 21 cm, a pole tego trójkąta jest równe 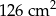 . Jaką długość ma najkrótsza z wysokości tego trójkąta?
. Jaką długość ma najkrótsza z wysokości tego trójkąta?
Z pięciu prostopadłościennych klocków o jednakowych wymiarach ułożono figurę. Kształt i wybrane wymiary tej figury przedstawiono na rysunku.
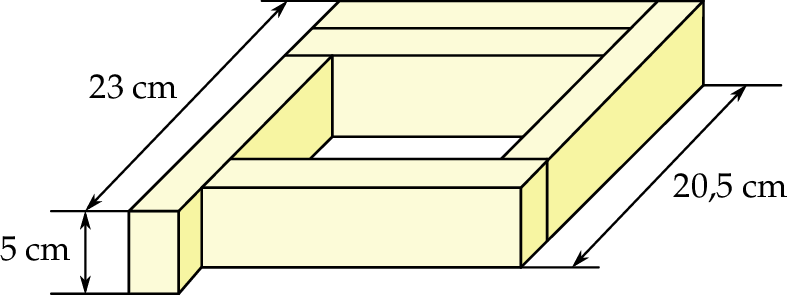
Oblicz objętość jednego klocka.
Z pięciu prostopadłościennych klocków o jednakowych wymiarach ułożono figurę. Kształt i wybrane wymiary tej figury przedstawiono na rysunku.
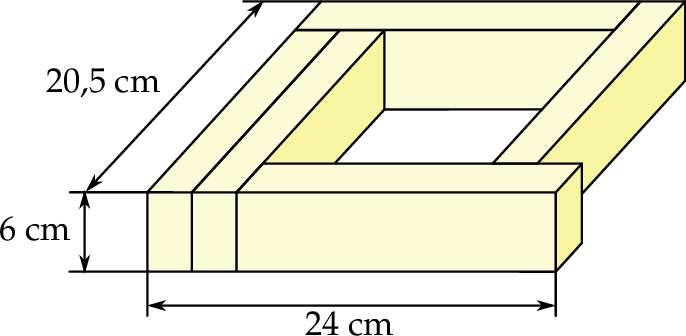
Oblicz objętość jednego klocka.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest większa od miary drugiego o 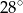 .
.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest większa od miary drugiego o 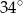 .
.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest 5 razy większa od miary drugiego.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest 4 razy większa od miary drugiego.
Prosta 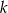 przechodzi przez punkty
przechodzi przez punkty 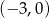 i
i 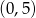 . Ustal w jakich punktach przecina osie układu współrzędnych prosta, która jest symetryczna do prostej
. Ustal w jakich punktach przecina osie układu współrzędnych prosta, która jest symetryczna do prostej 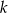 względem:
względem:
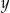 ;
;  ;
; Wysokość 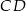 trójkąta
trójkąta 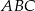 tworzy z bokami
tworzy z bokami 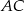 i
i 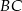 kąty o miarach równych odpowiednio
kąty o miarach równych odpowiednio 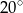 i
i 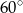 . Punkt
. Punkt 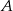 należy do odcinka
należy do odcinka 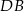 .
.
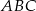 i jego wysokość
i jego wysokość 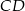 .
. 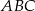 .
.W układzie współrzędnych na płaszczyźnie dane są punkty: 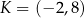 i
i 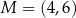 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 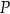 takiego, że jeden z trzech punktów
takiego, że jeden z trzech punktów 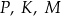 jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
Prostokąt o bokach długości 12 i 6 podzielono na dwa prostokąty (zobacz rysunek). Obwód jednego z prostokątów otrzymanych w wyniku podziału jest 2 razy większy od obwodu drugiego prostokąta.

Oblicz wymiary prostokąta o mniejszym obwodzie.
Jakie wielokąty mogą być podstawami ostrosłupa prawidłowego, w którym wszystkie krawędzie mają jednakową długość?
Ile ścian bocznych ma ostrosłup o 100 krawędziach?
Czy ostrosłup może mieć 22 krawędzie i 12 ścian bocznych?
Czy ostrosłup może mieć 15 krawędzi?
Bok rombu ma długość 13 cm, a jedna z przekątnych ma długość 24 cm. Oblicz pole tego rombu.
Bok rombu ma długość 10 cm, a jedna z przekątnych ma długość 16 cm. Oblicz pole tego rombu.
Punkty 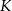 i
i 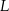 są środkami boków
są środkami boków 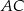 i
i 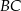 trójkąta
trójkąta 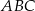 . Odcinki
. Odcinki 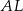 i
i 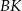 przecinają się w punkcie
przecinają się w punkcie 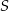 .
.
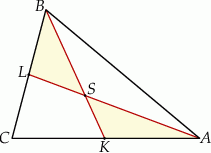
Uzasadnij, że pola trójkątów 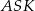 i
i 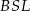 są równe.
są równe.
Sprawdź czy trójkąt jest prostokątny, jeżeli jego boki mają długości: 8 cm, 10 cm, 12 cm.
Sprawdź czy trójkąt jest prostokątny, jeżeli jego boki mają długości: 15 dm, 9 dm, 12 dm.
Punkt 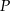 jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt
jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 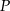 z wierzchołkiem trójkąta ma długość
z wierzchołkiem trójkąta ma długość 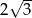 ?
?
Punkt 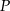 jest punktem przecięcia wysokości trójkąta równobocznego. Jaki obwód ma ten trójkąt jeśli odległość punktu
jest punktem przecięcia wysokości trójkąta równobocznego. Jaki obwód ma ten trójkąt jeśli odległość punktu 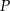 od jego boków jest równa
od jego boków jest równa 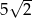 ?
?
Czy z odcinków o długościach: 4 cm, 4 cm, 9 cm można zbudować trójkąt?
Czy z odcinków o długościach: 3 cm, 3 cm, 3 cm można zbudować trójkąt?
Czy z odcinków o długościach: 4 cm, 4 cm, 2 cm można zbudować trójkąt?
Czy z odcinków o długościach: 3 cm, 7 cm, 4 cm można zbudować trójkąt?
Czy z odcinków o długościach: 11 cm, 8 cm, 17 cm można zbudować trójkąt?
Czy z odcinków o długościach: 8 cm, 13 cm, 20 cm można zbudować trójkąt?
Czy z odcinków o długościach: 13 cm, 8 cm, 5 cm można zbudować trójkąt?
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 15 cm, a przeciwprostokątna jest o 9 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 10 cm, a przeciwprostokątna jest o 2 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
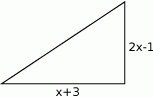
Pole trójkąta przedstawionego na rysunku jest równe 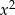 . Oblicz
. Oblicz  .
.
Z trzech jednakowych klocków w kształcie sześcianu i jednego klocka w kształcie ostrosłupa prawidłowego czworokątnego zbudowano dwie wieże (zobacz rysunek).
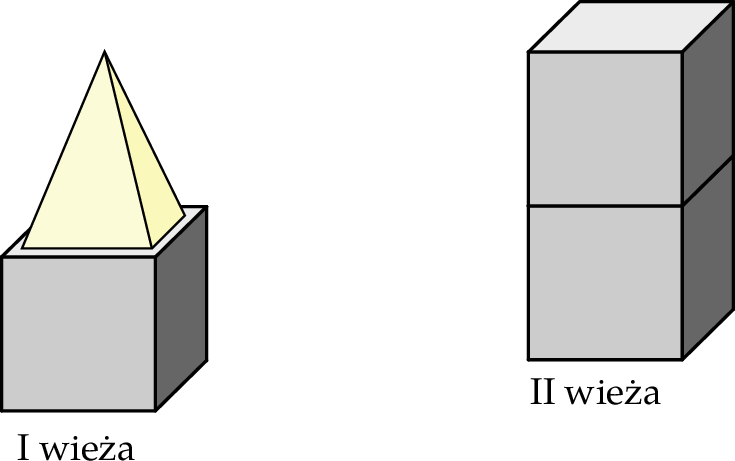
Krawędź sześcianu ma długość 10 cm. Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 9 cm, a jego objętość jest równa 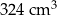 . Oblicz różnicę wysokości obu wież.
. Oblicz różnicę wysokości obu wież.
Obwód czworokąta wypukłego 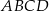 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 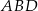 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 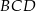 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 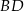 .
.
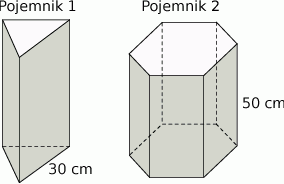
Dwa pojemniki mają kształt graniastosłupów prawidłowych, przy czym pierwszy ma kształt graniastosłupa trójkątnego o krawędzi podstawy długości 30 cm, a drugi sześciokątnego o wysokości 50 cm. Objętość pierwszego pojemnika stanowi 45% objętości drugiego pojemnika i jest mniejsza od tej objętości o 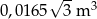 . Oblicz objętości obu pojemników.
. Oblicz objętości obu pojemników.