/Szkoła średnia/Równania/Trygonometryczne/Z tangensem

Zadanie nr 2934361

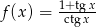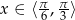Dana jest funkcja 1+tgx- f(x ) = ctgx dla π- π- x ∈ ⟨6 ,3⟩ .

Rozwiąż równanie .
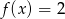Wyznacz najmniejszą wartość funkcji .

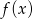Rozwiązanie

Korzystając z równości 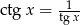mamy
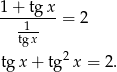
$1+--tg-x-= 2 -1- tgx tgx + tg2 x = 2.$

Podstawiając 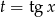mamy

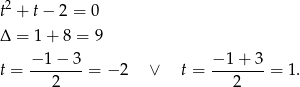
$2 t + t− 2 = 0 Δ = 1+ 8 = 9 t = −-1-−-3 = − 2 ∨ t = −-1-+-3 = 1 . 2 2$

Ze względu na dziedzinę funkcji 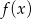tangens jest dodatni, więc mamy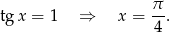

$π tgx = 1 ⇒ x = --. 4$

Odpowiedź: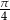
Z poprzedniego podpunktu wiemy, że
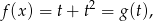
$2 f(x ) = t+ t = g (t),$

gdzie 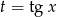. Ponieważ 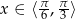, 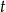przyjmuje wartości z przedziału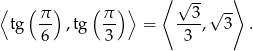

$⟨ ( ) ( ) ⟩ ⟨ √ -- ⟩ π- π- ---3 √ -- tg 6 ,tg 3 = 3 , 3 .$

(tu korzystamy z tego, że tangens jest rosnący na tym przedziale). Musimy więc wyznaczyć najmniejszą wartość funkcji 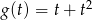na przedziale 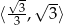. Ponieważ wierzchołek tej paraboli jest w punkcie 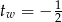, w interesującym nas przedziale jest to funkcja rosnąca. Zatem najmniejszą wartość przyjmuje w lewym końcu przedziału, czyli dla 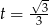, co nam daje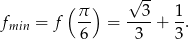

$√ -- (π-) --3- 1- fmin = f 6 = 3 + 3 .$

Odpowiedź:

Rozwiązanie Losuj ponownie