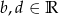Zadanie nr 3618875
Znaleźć wszystkie macierze kwadratowe przemienne z macierzą ![[ ] 2 − 1 A = 3 − 1](https://img.zadania.info/zad/3618875/HzadT0x.gif) .
.
Rozwiązanie
Szukamy macierzy 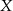 która spełnia warunek
która spełnia warunek
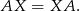
Aby te mnożenia miały sens, macierz 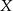 musi być wymiaru 2x2, czyli
musi być wymiaru 2x2, czyli
![[a b] X = c d](https://img.zadania.info/zad/3618875/HzadR3x.gif)
Ze wzoru na iloczyn macierzy mamy równanie
![[ ] [ ] [ ] [ ] 2 − 1 ⋅ a b = a b ⋅ 2 − 1 [3 − 1 c d] [ c d 3 − 1] 2a − c 2b − d 2a + 3b −a − b 3a − c 3b − d = 2c + 3d −c − d ( | 2a− c = 2a + 3b ||{ 3a− c = 2c + 3d || 2b− d = −a − b |( 3b− d = −c − d (| c = − 3b ||{ 3a = 3c + 3d || 3b = d − a |( − 3b = c](https://img.zadania.info/zad/3618875/HzadR4x.gif)
Podstawiając w drugim równaniu 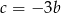 można zobaczyć, że jest ono identyczne jak trzecie. Pozostaje nam więc
można zobaczyć, że jest ono identyczne jak trzecie. Pozostaje nam więc
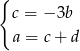
Możemy zatem wziąć dowolne 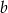 i
i 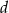 i mamy wtedy
i mamy wtedy 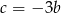 ,
, 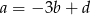 .
.
Odpowiedź: ![[ ] − 3b+ d b − 3b d](https://img.zadania.info/zad/3618875/HzadR11x.gif) ,
,