Zadanie nr 5163050
Zbadaj liczbę rozwiązań równania 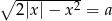 w zależności od wartości parametru
w zależności od wartości parametru  .
.
Rozwiązanie
Oczywiście jeżeli 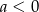 to równanie nie ma rozwiązań. Załóżmy więc, że
to równanie nie ma rozwiązań. Załóżmy więc, że 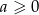 . Możemy wtedy podnieść równanie stronami do kwadratu (w zasadzie zawsze możemy podnieść, ale dzięki temu, że obie strony są dodatnie otrzymany równanie równoważne wyjściowemu).
. Możemy wtedy podnieść równanie stronami do kwadratu (w zasadzie zawsze możemy podnieść, ale dzięki temu, że obie strony są dodatnie otrzymany równanie równoważne wyjściowemu).
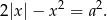
Sposób I
Najprostsze możliwe rozwiązanie, to naszkicowanie wykresu funkcji
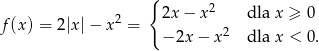
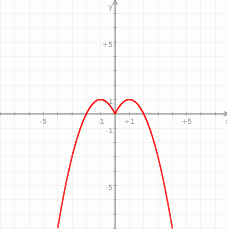
Z wykresu widać, że równanie 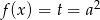

(przypominam, że interesują nas tylko dodatnie wartości 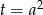 ). Ponieważ możemy jednoznacznie wyliczyć
). Ponieważ możemy jednoznacznie wyliczyć  z warunku
z warunku 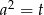 , równanie
, równanie 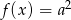 ma dokładnie tyle samo rozwiązań co równanie
ma dokładnie tyle samo rozwiązań co równanie 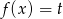 dla
dla 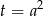 .
.
Sposób II
Zadanie można też rozwiązać algebraicznie. Mamy równanie
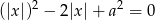
Podstawiając 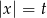 mamy
mamy
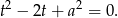
Sprawdźmy ile rozwiązań ma to równanie
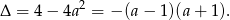
Widać więc, że dla 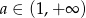 nie ma w ogóle rozwiązań (przypominam, że cały czas mamy założenie
nie ma w ogóle rozwiązań (przypominam, że cały czas mamy założenie 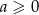 !). Musimy teraz sprawdzić co się dzieje w przedziale
!). Musimy teraz sprawdzić co się dzieje w przedziale 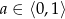 . Dla końców możemy sprawdzić wprost, dla
. Dla końców możemy sprawdzić wprost, dla 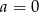 mamy
mamy 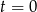 lub
lub 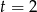 , co daje nam 3 wartości
, co daje nam 3 wartości  ; dla
; dla 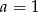 mamy
mamy 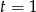 , co daje 2 wartości
, co daje 2 wartości  . Jeżeli natomiast
. Jeżeli natomiast 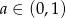 , to musimy się dokładniej zastanowić co jest grane – wiemy, że są dwa pierwiastki
, to musimy się dokładniej zastanowić co jest grane – wiemy, że są dwa pierwiastki 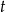 , ale nie wiemy ile dają one wartości
, ale nie wiemy ile dają one wartości  .
.
Jak wygląda parabola będąca wykresem powyższego równania? Pierwsza współrzędna jej wierzchołka to 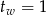 . Zatem na pewno jeden z pierwiastków jest na prawo od 1, więc da nam dwie wartości
. Zatem na pewno jeden z pierwiastków jest na prawo od 1, więc da nam dwie wartości  . Aby zobaczyć czy drugi pierwiastek jest dodatni czy ujemny liczymy
. Aby zobaczyć czy drugi pierwiastek jest dodatni czy ujemny liczymy 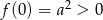 . Zatem oba pierwiastki są dodatnie i dadzą one 4 wartości
. Zatem oba pierwiastki są dodatnie i dadzą one 4 wartości  .
.
Odpowiedź: Liczba rozwiązań: