Zadanie nr 9294929
Rozwiąż równanie 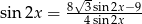 , gdzie
, gdzie 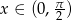 .
.
Rozwiązanie
Na początku zauważmy, że w podanym przedziale mianownik się nie zeruje, więc nie mamy kłopotu z dziedziną. Podstawiamy 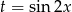 i przekształcamy
i przekształcamy
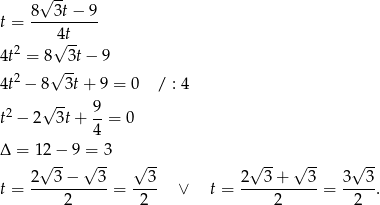
Drugie rozwiązanie odrzucamy, bo jest większe od 1 i dostajemy
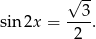
Teraz trzeba trochę uważać, bo niby szukamy rozwiązań w przedziale 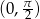 , ale
, ale 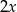 może już być w przedziale
może już być w przedziale 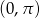 . Daje to nam dwa rozwiązania.
. Daje to nam dwa rozwiązania.
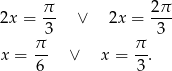
Odpowiedź: 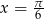 lub
lub