/Szkoła średnia/Funkcje - wykresy/Logarytmy/Różne

Zadanie nr 6391467

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla każdej liczby 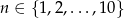n ∈ { 1,2,...,10} tworzymy funkcję 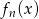fn(x) , której wykres powstaje przez przesunięcie wykresu funkcji 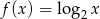f(x ) = lo g2x o wektor [0,−n ] .

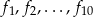  • Oblicz sumę wszystkich miejsc zerowych funkcji f ,f ,...,f 1 2 10 .
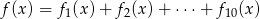  • Wyznacz miejsce zerowe funkcji f(x) = f1(x)+ f2(x)+ ⋅⋅⋅+ f10(x) .

Rozwiązanie

  • Ze wzoru na przesunięcie funkcji o wektor powinno być jasne, że
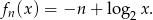
    fn(x) = −n + lo g2x.

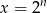    Miejsce zerowe tej funkcji to miejsce, w którym logarytm jest równy n , czyli x = 2n . Musimy zatem obliczyć sumę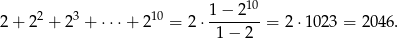

    10 2 + 22 + 23 + ⋅⋅⋅+ 210 = 2⋅ 1−--2-- = 2 ⋅1023 = 2046. 1− 2

     
    Odpowiedź: 2046

  • Mamy
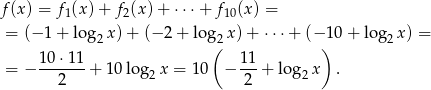
    f(x ) = f (x)+ f (x)+ ⋅⋅⋅+ f (x ) = 1 2 10 = (− 1 + log2 x)+ (− 2+ log 2x) + ⋅⋅⋅+ (− 10+ lo g2x ) = 1 0⋅11 ( 11 ) = − -------+ 10log2 x = 10 − ---+ log2 x . 2 2

    Zatem miejsce zerowe to

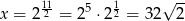
    x = 2 112-= 25 ⋅2 12 = 32√ 2

     
    Odpowiedź: √ -- x = 32 2

Wersja PDF
Rozwiązanie Losuj ponownie