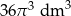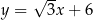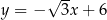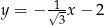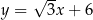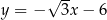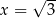Zbiór punktów płaszczyzny, których współrzędne spełniają równanie 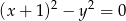 , jest
, jest
A) parabolą B) prostą C) okręgiem D) sumą dwóch prostych
/Szkoła średnia/Zadania testowe
Zbiór punktów płaszczyzny, których współrzędne spełniają równanie 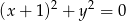 , jest
, jest
A) parabolą B) punktem C) okręgiem D) sumą dwóch prostych
Miara kąta wpisanego opartego na  okręgu wynosi:
okręgu wynosi:
A) 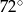 B)
B) 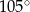 C)
C) 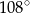 D)
D) 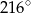
Miara kąta wpisanego opartego na  długości okręgu jest równa
długości okręgu jest równa
A) 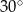 B)
B) 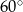 C)
C) 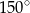 D)
D) 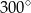
Jaką miarę ma kąt wpisany oparty na 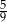 łuku okręgu?
łuku okręgu?
A) 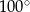 B)
B) 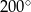 C)
C) 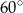 D)
D) 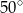
Kąt wpisany oparty jest na łuku, którego długość jest równa 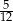 długości okręgu. Miara tego kąta wynosi
długości okręgu. Miara tego kąta wynosi
A) 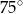 B)
B) 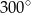 C)
C) 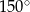 D)
D) 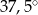
Miara kąta wpisanego opartego na łuku długości 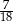 długości całego okręgu wynosi
długości całego okręgu wynosi
A) 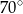 B)
B) 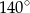 C)
C) 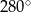 D)
D) 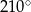
Liczba rozwiązań równania 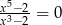 jest równa
jest równa
A) 0 B) 1 C) 2 D) 5
Liczba rozwiązań równania 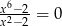 jest równa
jest równa
A) 6 B) 3 C) 2 D) 1
Kąt  jest ostry i
jest ostry i 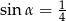 . Wówczas
. Wówczas
A) 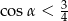 B)
B) 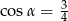 C)
C) 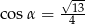 D)
D) 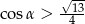
Kąt  jest ostry i
jest ostry i 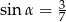 . Wówczas
. Wówczas
A) 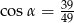 B)
B) 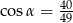 C)
C) 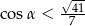 D)
D) 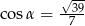
Liczba 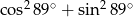 jest
jest
A) ujemna B) niewymierna C) parzysta D) nieparzysta
Liczba 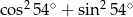 jest
jest
A) dodatnia B) niewymierna C) parzysta D) ujemna
Dane są dwa okręgi: okrąg o środku w punkcie 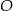 i promieniu 5 oraz okrąg o środku w punkcie
i promieniu 5 oraz okrąg o środku w punkcie 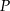 i promieniu 3. Odcinek
i promieniu 3. Odcinek 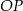 ma długość 16. Prosta
ma długość 16. Prosta 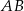 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 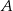 i
i 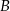 . Ponadto prosta
. Ponadto prosta 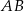 przecina odcinek
przecina odcinek 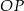 w punkcie
w punkcie 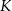 (zobacz rysunek).
(zobacz rysunek).
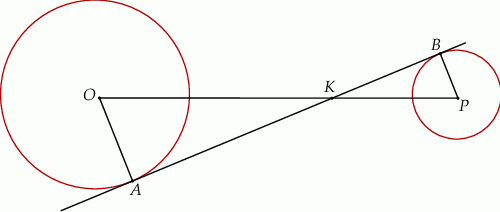
Wtedy
A) 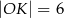 B)
B) 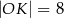 C)
C) 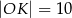 D)
D) 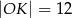
Dane są dwa okręgi: okrąg o środku w punkcie 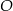 i promieniu 4 oraz okrąg o środku w punkcie
i promieniu 4 oraz okrąg o środku w punkcie 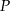 i promieniu 6. Odcinek
i promieniu 6. Odcinek 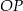 ma długość 25. Prosta
ma długość 25. Prosta 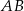 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 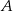 i
i 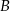 . Ponadto prosta
. Ponadto prosta 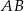 przecina odcinek
przecina odcinek 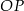 w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek).
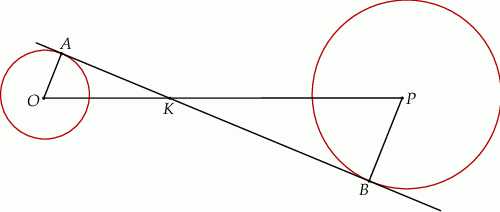
Wtedy
A) 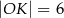 B)
B) 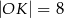 C)
C) 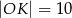 D)
D) 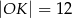
Jeśli promień podstawy stożka zwiększymy trzykrotnie, a wysokość zmniejszymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zwiększy się sześciokrotnie
Jeśli promień podstawy stożka zmniejszymy trzykrotnie, a wysokość zwiększymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zmniejszy się trzykrotnie
Jeśli promień podstawy stożka zwiększymy dwukrotnie, a wysokość zmniejszymy dwukrotnie, to objętość stożka
A) zwiększy się dwukrotnie B) nie zmieni się
C) zwiększy się czterokrotnie D) zmniejszy się czterokrotnie
Dany jest ciąg geometryczny 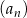 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 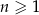 . Drugi wyraz tego ciągu oraz iloraz ciągu
. Drugi wyraz tego ciągu oraz iloraz ciągu 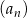 są równe 2. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
są równe 2. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 1 B) 11 C) 21 D) 31
Dany jest ciąg geometryczny 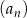 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 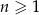 . Drugi wyraz tego ciągu oraz iloraz ciągu
. Drugi wyraz tego ciągu oraz iloraz ciągu 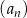 są równe
są równe 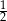 . Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 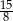 B)
B) 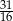 C)
C) 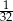 D)
D) 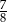
Końce odcinka  o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
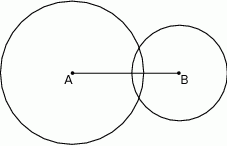
Punkt  leży na odcinku
leży na odcinku 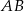 i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku
i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku 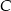 ma długość
ma długość
A) 6,5 B) 7,5 C) 8,5 D) 9,5
Która z poniższych funkcji nie ma ekstremów lokalnych?
A) 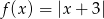 B)
B) 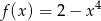 C)
C) 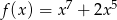 D)
D) 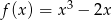
Która z poniższych funkcji nie ma ekstremów lokalnych?
A) 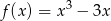 B)
B) 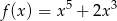 C)
C) 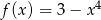 D)
D) 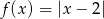
W kartezjańskim układzie współrzędnych 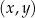 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 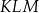 . Trójkąt
. Trójkąt 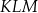 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 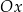 przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | oś 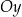 zawiera dwusieczną tego trójkąta. zawiera dwusieczną tego trójkąta. |
W kartezjańskim układzie współrzędnych 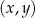 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 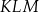 . Trójkąt
. Trójkąt 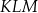 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 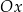 jest osią symetrii tego trójkąta. jest osią symetrii tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | jedna z tych prostych jest równoległa do osi 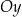 . . |
Jeżeli  jest kątem wewnętrznym trójkąta
jest kątem wewnętrznym trójkąta 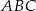 i
i 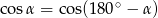 , to trójkąt
, to trójkąt 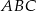 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
Iloczyn liczb spełniających równanie 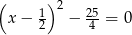 jest równy
jest równy
A) 6 B) 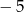 C) 5 D)
C) 5 D) 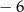
Funkcja kwadratowa określona jest wzorem 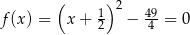 . Liczby
. Liczby 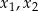 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 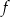 . Zatem
. Zatem
A) 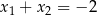 B)
B) 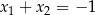 C)
C) 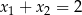 D)
D) 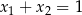
Ciąg 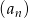 o wyrazie ogólnym
o wyrazie ogólnym 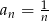 jest ciągiem
jest ciągiem
A) malejącym B) arytmetycznym C) rosnącym D) geometrycznym
Ciąg 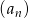 o wyrazie ogólnym
o wyrazie ogólnym 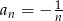 jest ciągiem
jest ciągiem
A) malejącym B) arytmetycznym C) rosnącym D) geometrycznym
Ciąg 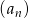 o wyrazie ogólnym
o wyrazie ogólnym 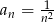 jest ciągiem
jest ciągiem
A) arytmetycznym B) malejącym C) rosnącym D) geometrycznym
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 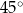 (zobacz rysunek).
(zobacz rysunek).
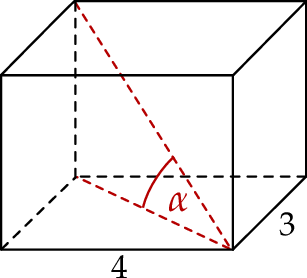
Wysokość graniastosłupa jest równa
A) 5 B) 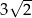 C)
C) 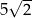 D)
D) 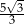
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki tworzą dwie przekątne tego graniastosłupa, jest równy
, jaki tworzą dwie przekątne tego graniastosłupa, jest równy 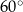 (zobacz rysunek).
(zobacz rysunek).
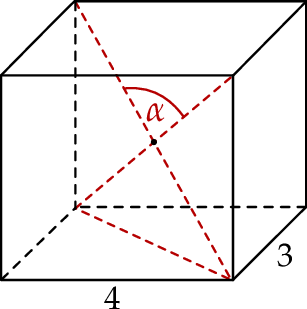
Wysokość graniastosłupa jest równa
A) 10 B) 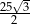 C)
C) 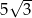 D)
D) 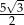
Graniastosłup prosty ma pole powierzchni całkowitej równe 94, a w jego podstawie jest prostokąt o bokach długości 3 i 4 (zobacz rysunek).
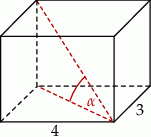
Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
A) 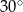 B)
B) 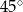 C)
C) 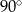 D)
D) 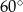
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 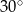 (zobacz rysunek).
(zobacz rysunek).
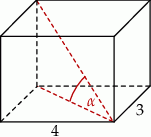
Wysokość graniastosłupa jest równa
A) 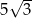 B)
B) 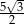 C)
C) 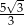 D)
D) 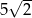
Średnia arytmetyczna zestawu liczb: 13, 16, 11, 4, 7, 9 zwiększy się o 25%, gdy w miejsce 7 wpiszemy liczbę
A) 75 B) 2,5 C) 15 D) 22
Średnia arytmetyczna zestawu liczb: 12, 5, 13, 9, 2, 7 zwiększy się o 75%, gdy w miejsce 2 wpiszemy liczbę
A) 36 B) 84 C) 38 D) 14
Do wykresu funkcji liniowej 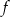 należą punkty
należą punkty 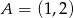 i
i 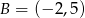 . Funkcja
. Funkcja 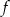 ma wzór
ma wzór
A) 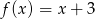 B)
B) 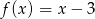 C)
C) 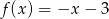 D)
D) 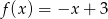
Przez punkty 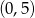 i
i 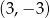 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 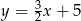 B)
B) 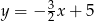 C)
C) 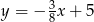 D)
D) 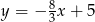
Do wykresu funkcji liniowej 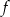 należą punkty
należą punkty 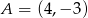 i
i 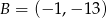 . Funkcja
. Funkcja 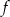 opisana jest wzorem
opisana jest wzorem
A) 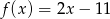 B)
B) 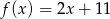 C)
C) 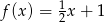 D)
D) 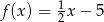
Do wykresu funkcji liniowej 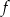 należą punkty
należą punkty 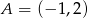 i
i 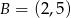 . Funkcja
. Funkcja 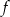 ma wzór
ma wzór
A) 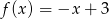 B)
B) 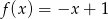 C)
C) 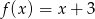 D)
D) 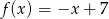
Do wykresu funkcji liniowej 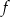 należą punkty
należą punkty 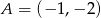 i
i 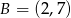 . Funkcja
. Funkcja 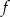 ma wzór
ma wzór
A) 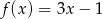 B)
B) 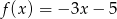 C)
C) 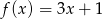 D)
D) 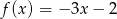
O funkcji liniowej 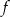 wiadomo, że
wiadomo, że 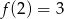 oraz punkt
oraz punkt 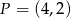 należy do jej wykresu. Wzór funkcji
należy do jej wykresu. Wzór funkcji 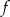 to
to
A) 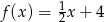 B)
B) 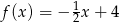 C)
C) 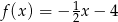 D)
D) 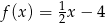
O funkcji liniowej 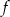 wiadomo, że
wiadomo, że 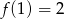 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 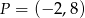 . Wzór funkcji
. Wzór funkcji 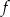 to
to
A) 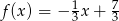 B)
B) 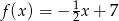 C)
C) 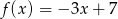 D)
D) 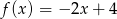
Przez punkty 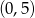 i
i 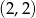 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 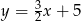 B)
B) 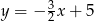 C)
C) 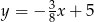 D)
D) 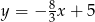
Przez punkty 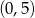 i
i 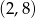 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 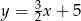 B)
B)  C)
C) 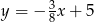 D)
D) 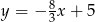
O funkcji liniowej 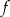 wiadomo, że
wiadomo, że 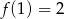 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 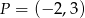 . Wzór funkcji
. Wzór funkcji 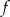 to
to
A) 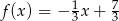 B)
B) 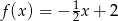 C)
C) 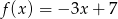 D)
D) 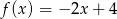
Miara kąta  wynosi
wynosi
A) 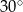 B)
B) 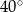 C)
C) 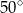 D)
D) 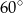
Punkty 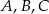 i
i 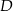 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 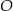 . Cięciwy
. Cięciwy 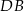 i
i 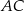 przecinają się w punkcie
przecinają się w punkcie 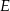 ,
, 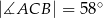 oraz
oraz 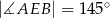 (zobacz rysunek).
(zobacz rysunek).
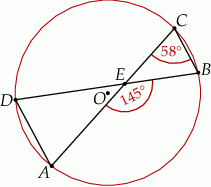
Miara kąta 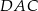 jest równa
jest równa
A) 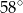 B)
B) 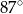 C)
C) 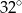 D)
D) 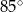
Punkty 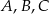 i
i 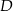 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 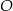 . Cięciwy
. Cięciwy 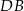 i
i 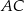 przecinają się w punkcie
przecinają się w punkcie 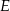 ,
, 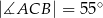 oraz
oraz 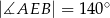 (zobacz rysunek).
(zobacz rysunek).
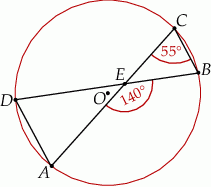
Miara kąta 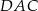 jest równa
jest równa
A) 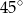 B)
B) 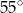 C)
C) 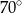 D)
D) 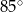
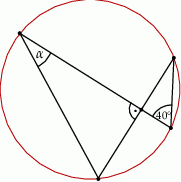
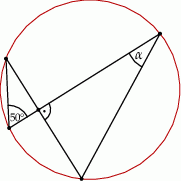
Kąt  na rysunku obok ma miarę
na rysunku obok ma miarę
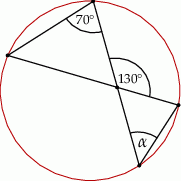
A) 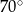 B)
B) 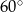 C)
C) 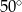 D)
D) 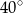
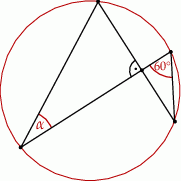
Miara kąta  wynosi
wynosi
A) 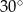 B)
B) 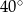 C)
C) 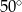 D)
D) 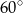
Miara kąta  wynosi
wynosi
A) 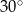 B)
B) 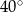 C)
C) 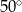 D)
D) 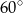
Wskaż funkcję, która nie przyjmuje wartości ujemnych
A) 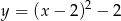 B)
B) 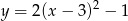 C)
C) 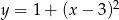 D)
D) 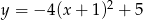
Wskaż funkcję, która nie przyjmuje wartości ujemnych
A) 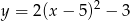 B)
B) 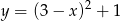 C)
C) 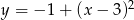 D)
D) 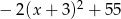
Objętość kuli o promieniu 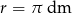 jest równa
jest równa
A) 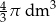 B)
B) 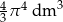 C)
C) 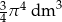 D)
D) 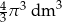
Objętość kuli o promieniu 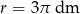 jest równa
jest równa
A) 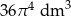 B)
B) 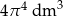 C)
C) 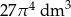 D)
D)