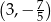Jedną z liczb, które nie spełniają nierówność 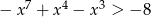 , jest
, jest
A) 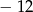 B)
B) 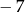 C) 20 D)
C) 20 D) 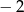
/Szkoła średnia/Zadania testowe
W trójkącie równoramiennym 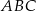 o podstawie
o podstawie 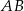 dane są:
dane są: 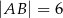 oraz
oraz 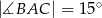 . Pole koła opisanego na tym trójkącie jest równe
. Pole koła opisanego na tym trójkącie jest równe
A) 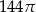 B)
B) 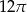 C)
C) 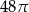 D)
D) 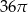
Funkcja kwadratowa określona jest wzorem 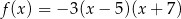 . Funkcja ta jest rosnąca w przedziale:
. Funkcja ta jest rosnąca w przedziale:
A) 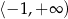 B)
B) 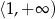 C)
C) 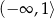 D)
D) 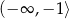
Dana jest funkcja kwadratowa 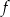 określona wzorem
określona wzorem 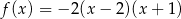 . Funkcja
. Funkcja 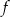 jest rosnąca w zbiorze
jest rosnąca w zbiorze
A) 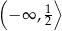 B)
B) 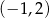 C)
C) 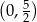 D)
D) 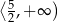
Funkcja kwadratowa 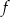 określona wzorem
określona wzorem 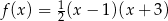 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 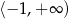 B)
B) 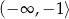 C)
C) 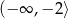 D)
D) 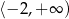
Funkcja kwadratowa 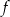 określona jest wzorem
określona jest wzorem 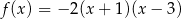 jest malejąca w przedziale
jest malejąca w przedziale
A) 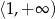 B)
B) 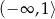 C)
C) 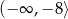 D)
D) 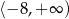
Funkcja kwadratowa określona jest wzorem 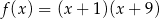 . Wynika stąd, że funkcja
. Wynika stąd, że funkcja 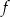 jest malejąca w przedziale
jest malejąca w przedziale
A) 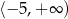 B)
B) 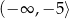 C)
C) 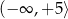 D)
D) 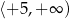
Funkcja kwadratowa 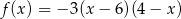 jest malejąca w przedziale
jest malejąca w przedziale
A) 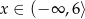 B)
B) 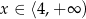 C)
C) 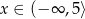 D)
D) 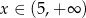
Dana jest funkcja kwadratowa 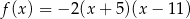 . Wskaż maksymalny przedział, w którym funkcja
. Wskaż maksymalny przedział, w którym funkcja 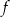 jest rosnąca.
jest rosnąca.
A) 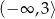 B)
B) 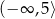 C)
C) 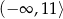 D)
D) 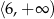
Funkcja kwadratowa określona jest wzorem 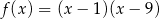 . Wynika stąd, że funkcja
. Wynika stąd, że funkcja 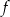 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 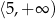 B)
B) 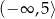 C)
C) 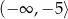 D)
D) 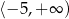
Dana jest funkcja kwadratowa 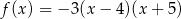 . Wskaż maksymalny przedział, w którym funkcja
. Wskaż maksymalny przedział, w którym funkcja 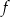 jest malejąca.
jest malejąca.
A) 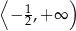 B)
B) 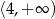 C)
C) 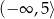 D)
D) 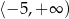
Funkcja kwadratowa 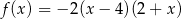 jest malejąca w przedziale
jest malejąca w przedziale
A) 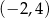 B)
B) 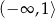 C)
C) 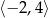 D)
D) 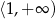
Wiadomo, że 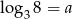 i
i 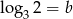 . Wynika stąd, że
. Wynika stąd, że
A) 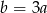 B)
B) 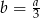 C)
C) 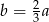 D)
D) 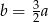
W ciągu arytmetycznym 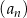 określonym dla
określonym dla 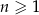 , średnia arytmetyczna wyrazów:
, średnia arytmetyczna wyrazów: 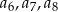 jest o 33 mniejsza od średniej arytmetycznej wyrazów
jest o 33 mniejsza od średniej arytmetycznej wyrazów 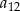 i
i 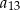 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 6 B) 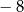 C)
C) 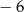 D) 8
D) 8
Średnia arytmetyczna dziesięciu kolejnych liczb naturalnych jest równa 15,5. Mediana tych liczb jest równa
A) 15,5 B) 31 C) 16 D) 16,5
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 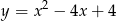 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 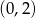 B)
B) 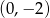 C)
C) 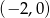 D)
D) 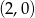
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 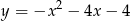 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 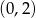 B)
B) 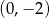 C)
C) 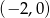 D)
D) 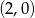
Wykresem funkcji kwadratowej 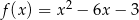 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 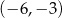 B)
B) 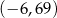 C)
C) 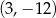 D)
D) 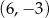
Wykresem funkcji kwadratowej 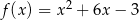 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 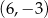 B)
B) 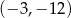 C)
C) 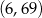 D)
D) 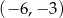
Wykresem funkcji kwadratowej 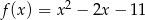 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 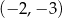 B)
B) 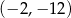 C)
C) 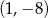 D)
D) 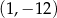
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
A) 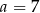 B)
B) 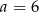 C)
C) 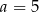 D)
D) 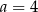
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
A) 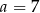 B)
B) 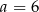 C)
C) 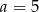 D)
D) 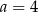
Jedno rozwiązanie ma równanie
A) 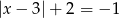 B)
B) 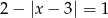 C)
C) 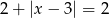 D)
D) 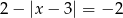
Dziewiąty wyraz ciągu geometrycznego jest równy 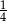 , a iloraz tego ciągu jest równy
, a iloraz tego ciągu jest równy 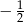 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 16 B) 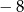 C)
C) 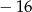 D) 8
D) 8
W trójkącie równoramiennym o bokach długości: 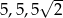 kąt przy podstawie ma miarę:
kąt przy podstawie ma miarę:
A) 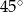 B)
B) 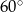 C)
C) 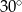 D)
D) 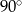
Wyrażenie 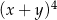 jest równe
jest równe
A) 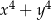 B)
B) 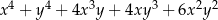
C) 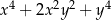 D)
D) 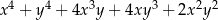
Wyrażenie 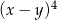 jest równe
jest równe
A) 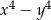 B)
B) 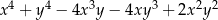
C) 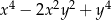 D)
D) 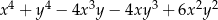
Suma przedziałów 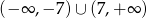 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 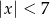 B)
B) 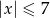 C)
C) 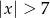 D)
D) 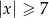
Suma przedziałów 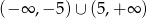 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 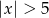 B)
B) 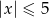 C)
C) 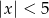 D)
D) 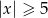
Suma przedziałów 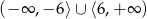 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 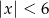 B)
B) 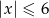 C)
C) 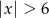 D)
D) 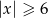
Podstawą ostrosłupa jest kwadrat 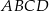 o boku długości 1. Wysokością tego ostrosłupa jest krawędź
o boku długości 1. Wysokością tego ostrosłupa jest krawędź 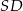 , a długość krawędzi
, a długość krawędzi 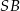 jest równa 2 (zobacz rysunek).
jest równa 2 (zobacz rysunek).
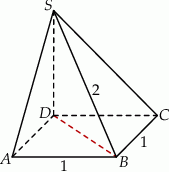
Różnica miar kątów 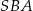 i
i 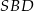 jest równa
jest równa
A) 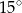 B)
B) 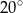 C)
C) 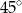 D)
D) 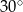
Objętość walca wynosi 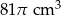 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 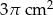 B)
B) 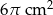 C)
C) 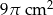 D)
D) 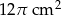
Ciąg 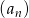 określony jest wzorem
określony jest wzorem 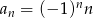 , gdzie
, gdzie 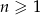 . Wówczas wyrażenie
. Wówczas wyrażenie 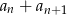 jest równe
jest równe
A) 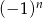 B)
B) 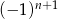 C)
C) 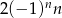 D)
D) 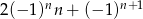
Objętość sześcianu jest równa 64. Pole powierzchni całkowitej tego sześcianu jest równe
A) 512 B) 384 C) 96 D) 16
Wszystkich par 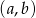 takich, że
takich, że 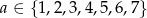 ,
, 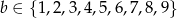 oraz suma
oraz suma 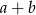 jest podzielna przez 3, jest
jest podzielna przez 3, jest
A) mniej niż 21 B) dokładnie 21 C) dokładnie 22 D) więcej niż 22
Stężenie roztworu początkowo wzrosło o 30%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 50% C) 56% D) 60%
Stężenie roztworu początkowo wzrosło o 25%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 45% B) 50% C) 55% D) 60%
Stężenie roztworu początkowo wzrosło o 20%, a po 15 minutach wzrosło o dalsze 30%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 56% C) 50% D) 60%
Wykresem funkcji kwadratowej 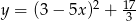 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 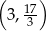 B)
B) 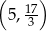 C)
C) 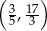 D)
D) 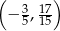
Wykresem funkcji kwadratowej 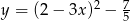 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 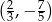 B)
B) 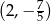 C)
C) 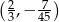 D)
D)