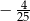Prostą równoległą do prostej 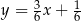 jest prosta:
jest prosta:
A) 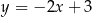 B)
B) 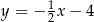 C)
C) 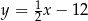 D)
D) 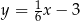
/Szkoła średnia/Zadania testowe
Wskaż równanie prostej równoległej do prostej o równaniu 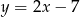 .
.
A) 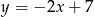 B)
B) 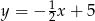 C)
C) 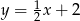 D)
D) 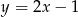
Prosta o równaniu 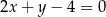 jest równoległa do prostej:
jest równoległa do prostej:
A) 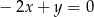 B)
B) 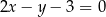 C)
C) 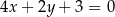 D)
D) 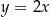
Prostą równoległą do prostej 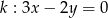 opisuje równanie
opisuje równanie
A) 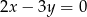 B)
B) 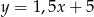 C)
C) 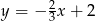 D)
D) 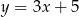
Dana jest prosta 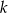 o równaniu
o równaniu 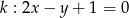 . Spośród podanych prostych wybierz prostą równoległą do
. Spośród podanych prostych wybierz prostą równoległą do 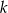 .
.
A) 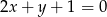 B)
B) 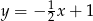 C)
C) 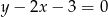 D)
D) 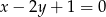
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 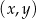 , dana jest prosta
, dana jest prosta 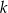 o równaniu
o równaniu 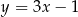 . Jedną z prostych równoległych do prostej
. Jedną z prostych równoległych do prostej 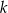 jest prosta o równaniu
jest prosta o równaniu
A) 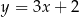 B)
B) 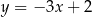 C)
C) 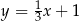 D)
D) 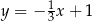
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 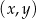 , dana jest prosta
, dana jest prosta 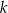 o równaniu
o równaniu 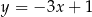 . Jedną z prostych równoległych do prostej
. Jedną z prostych równoległych do prostej 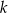 jest prosta o równaniu
jest prosta o równaniu
A) 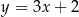 B)
B) 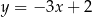 C)
C) 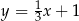 D)
D) 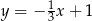
Prostą równoległą do prostej o równaniu 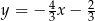 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 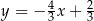 B)
B) 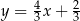 C)
C) 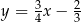 D)
D) 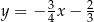
Wskaż równanie prostej równoległej do prostej o równaniu 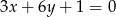 .
.
A) 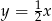 B)
B) 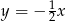 C)
C) 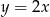 D)
D) 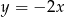
Prosta 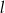 ma równanie
ma równanie 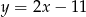 . Wskaż równanie prostej równoległej do
. Wskaż równanie prostej równoległej do 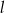 .
.
A) 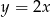 B)
B) 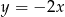 C)
C) 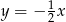 D)
D) 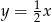
Prosta 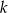 równoległa do prostej
równoległa do prostej 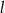 o równaniu
o równaniu 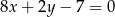 może mieć wzór
może mieć wzór
A) 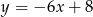 B)
B) 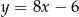 C)
C) 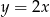 D)
D) 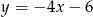
Prostą równoległą do prostej o równaniu 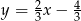 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 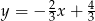 B)
B) 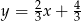 C)
C) 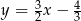 D)
D) 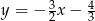
Wskaż równanie prostej równoległej do prostej o równaniu 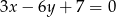 .
.
A) 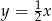 B)
B) 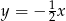 C)
C) 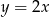 D)
D) 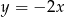
Prosta równoległa do prostej 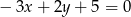 ma równanie:
ma równanie:
A) 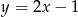 B)
B) 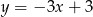 C)
C) 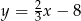 D)
D) 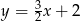
Miejscami zerowymi funkcji kwadratowej 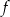 są liczby
są liczby 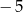 i 6, a miejscami zerowymi funkcji
i 6, a miejscami zerowymi funkcji 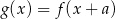 są liczby 1 i 12. Wynika stąd, że
są liczby 1 i 12. Wynika stąd, że
A) 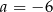 B)
B) 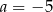 C)
C) 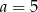 D)
D) 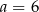
Jeden z kątów ostrych trójkąta prostokątnego ma miarę 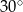 . Dłuższa przyprostokątna tego trójkąta ma długość 6 cm. Promień okręgu opisanego na tym trójkącie ma długość
. Dłuższa przyprostokątna tego trójkąta ma długość 6 cm. Promień okręgu opisanego na tym trójkącie ma długość
A) 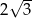 B) 6 C)
B) 6 C) 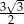 D)
D) 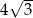
Dziedziną funkcji 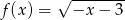 jest zbiór
jest zbiór
A) 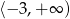 B)
B) 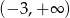 C)
C) 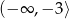 D)
D) 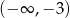
Dziedziną funkcji 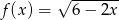 jest przedział
jest przedział
A) 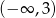 B)
B) 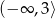 C)
C) 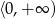 D)
D) 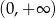
Dziedziną funkcji 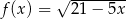 jest zbiór
jest zbiór
A) 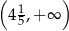 B)
B) 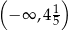 C)
C) 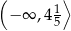 D)
D) 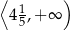
Dziedziną funkcji 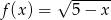 jest zbiór
jest zbiór
A) 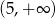 B)
B) 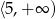 C)
C) 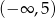 D)
D) 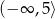
Suma odległości wierzchołka paraboli o równaniu 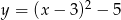 od osi układu współrzędnych jest równa
od osi układu współrzędnych jest równa
A) 4 B) 3 C) 5 D) 8
Suma odległości wierzchołka paraboli o równaniu 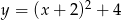 od osi układu współrzędnych jest równa
od osi układu współrzędnych jest równa
A) 6 B) 2 C) -2 D) -6
Kąt  jest ostry i
jest ostry i 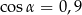 . Wówczas
. Wówczas
A) 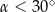 B)
B) 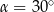 C)
C) 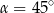 D)
D) 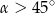
Kąt  jest ostry i
jest ostry i 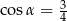 . Wówczas
. Wówczas
A) 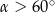 B)
B) 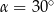 C)
C) 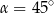 D)
D) 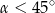
Kąt  jest kątem ostrym i
jest kątem ostrym i 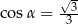 . Zatem
. Zatem
A) 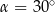 B)
B) 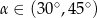 C)
C) 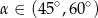 D)
D) 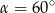
Średnią arytmetyczną liczb 5,5,7,3,9,9,4,4 jest liczba
A) 8 B) 5,5 C) 4 D) 5,75
Średnią arytmetyczną liczb 3,3,5,6,8,9,4,4 jest liczba
A) 6 B) 5,25 C) 5 D) 5,75
Średnią arytmetyczną liczb 6,6,5,3,8,8,4,4 jest liczba
A) 6 B) 5,5 C) 4 D) 5,75
W trójkącie 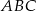 poprowadzono odcinek
poprowadzono odcinek 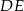 równoległy do boku
równoległy do boku 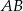 w ten sposób, że
w ten sposób, że 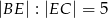 .
.
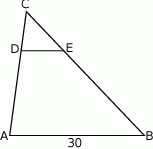
Jeżeli 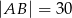 to długość odcinka
to długość odcinka 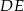 jest równa
jest równa
A) 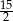 B) 6 C) 5 D)
B) 6 C) 5 D) 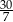
W trójkącie 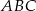 poprowadzono odcinek
poprowadzono odcinek 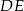 równoległy do boku
równoległy do boku 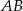 w ten sposób, że
w ten sposób, że 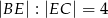 .
.
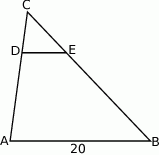
Jeżeli 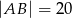 to długość odcinka
to długość odcinka 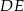 jest równa
jest równa
A) 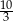 B) 4 C) 5 D)
B) 4 C) 5 D) 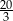
Wskaż równość prawdziwą.
A) 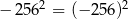 B)
B) 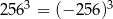
C) 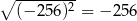 D)
D) 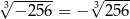
Wskaż równość fałszywą.
A) 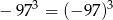 B)
B) 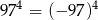 C)
C) 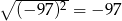 D)
D) 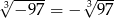
Dziedziną funkcji 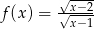 jest przedział
jest przedział
A) 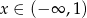 B)
B) 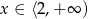 C)
C) 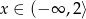 D)
D) 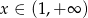
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 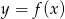 , której dziedziną jest zbiór
, której dziedziną jest zbiór 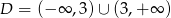 .
.
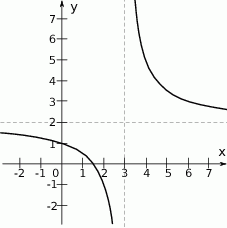
Równanie 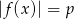 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 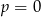 lub
lub 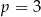 .
.
B) w dwóch przypadkach: 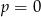 lub
lub 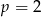 .
.
C) tylko wtedy, gdy 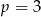 .
.
D) tylko wtedy, gdy 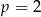 .
.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 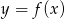 , której dziedziną jest zbiór
, której dziedziną jest zbiór 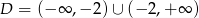 .
.
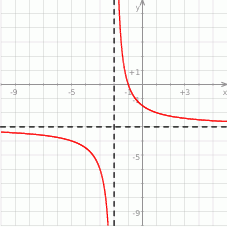
Równanie 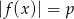 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 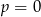 lub
lub 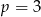 .
.
B) w dwóch przypadkach: 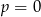 lub
lub 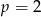 .
.
C) tylko wtedy, gdy 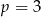 .
.
D) tylko wtedy, gdy 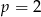 .
.
Pole prostokąta 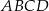 jest równe 90. Na bokach
jest równe 90. Na bokach 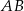 i
i 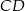 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 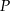 i
i 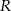 , takie, że
, takie, że 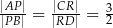 (zobacz rysunek)
(zobacz rysunek)
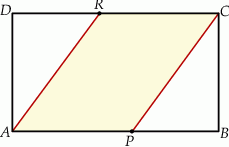
Pole czworokąta 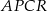 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Pole prostokąta 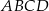 jest równe 90. Na bokach
jest równe 90. Na bokach 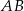 i
i 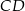 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 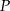 i
i 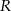 , takie, że
, takie, że 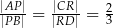 (zobacz rysunek)
(zobacz rysunek)
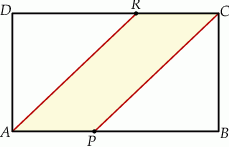
Pole czworokąta 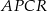 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Z punktu 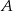 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 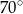 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 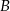 i
i 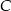 . Punkt
. Punkt 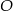 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 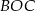 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 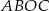 , jest równa
, jest równa
A) 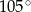 B)
B) 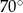 C)
C) 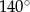 D)
D) 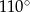
Z punktu 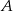 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 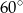 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 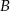 i
i 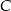 . Punkt
. Punkt 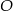 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 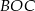 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 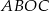 , jest równa
, jest równa
A) 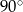 B)
B) 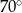 C)
C) 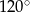 D)
D) 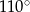
Z punktu 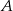 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 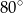 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 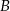 i
i 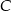 . Punkt
. Punkt 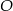 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 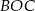 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 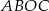 , jest równa
, jest równa
A) 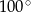 B)
B) 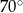 C)
C) 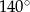 D)
D) 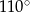
Końcami odcinka 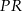 są punkty
są punkty 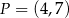 i
i 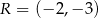 . Odległość punktu
. Odległość punktu 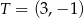 od środka odcinka
od środka odcinka 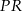 jest równa
jest równa
A) 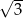 B)
B) 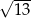 C)
C) 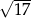 D)
D) 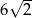
Końcami odcinka 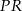 są punkty
są punkty 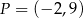 i
i 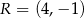 . Odległość punktu
. Odległość punktu 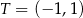 od środka odcinka
od środka odcinka 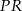 jest równa
jest równa
A) 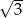 B)
B) 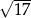 C)
C) 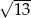 D)
D) 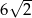
Na rysunku przedstawiono wykres funkcji 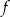 .
.
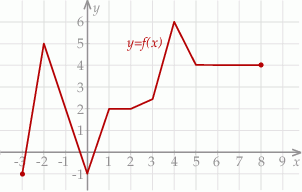
Najdłuższy przedział, na którym funkcja 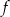 jest rosnąca to
jest rosnąca to
A) 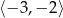 B)
B) 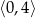 C)
C) 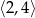 D)
D) 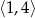
Na rysunku przedstawiono wykres funkcji 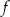 .
.
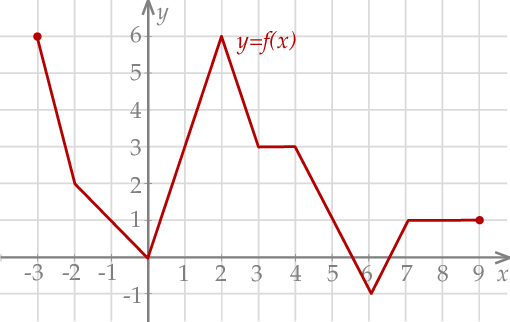
Najdłuższy przedział, na którym funkcja 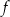 jest malejąca to
jest malejąca to
A) 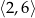 B)
B) 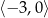 C)
C) 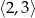 D)
D) 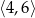
Liczby 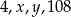 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 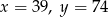 B)
B) 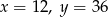 C)
C) 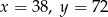 D)
D) 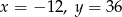
Liczby 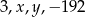 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 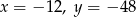 B)
B) 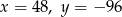 C)
C) 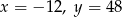 D)
D) 
Dane są dwie sumy algebraiczne 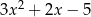 oraz
oraz 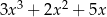 . Iloczyn tych sum jest równy
. Iloczyn tych sum jest równy
A) 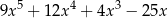 B)
B) 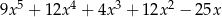
C) 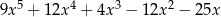 D)
D) 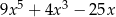
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna tego trójkąta ma długość
A) 24 B) 20 C) 14 D) 18
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 4. Wysokość ta dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna jest równa
A) 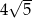 B)
B) 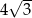 C) 10 D) 8
C) 10 D) 8
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 8 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 4. Przeciwprostokątna tego trójkąta ma długość
A) 20 B) 16 C) 8 D) 18
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 12. Przeciwprostokątna tego trójkąta ma długość
A) 15 B) 24 C) 16 D) 3
Na rysunku przedstawiono fragment wykresu pochodnej 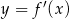 funkcji
funkcji 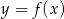 .
.
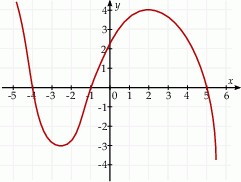
Funkcja 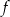 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 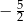 B)
B) 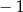 C)
C) 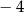 D) 2
D) 2
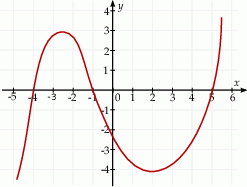
Na rysunku przedstawiono fragment wykresu pochodnej 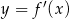 funkcji
funkcji 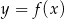 .
.
Funkcja 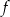 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 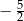 B)
B) 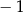 C)
C) 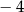 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 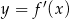 funkcji
funkcji 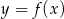 .
.
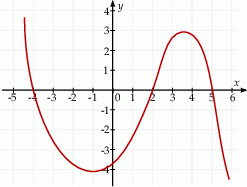
Funkcja 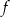 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A)  B)
B) 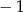 C)
C) 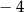 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 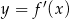 funkcji
funkcji 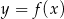 .
.
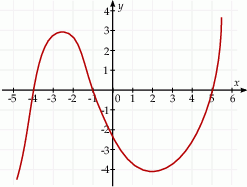
Funkcja 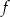 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 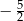 B)
B) 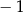 C)
C) 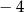 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 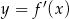 funkcji
funkcji 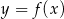 .
.
Funkcja 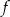 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A)  B)
B) 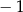 C)
C) 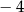 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 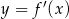 funkcji
funkcji 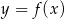 .
.
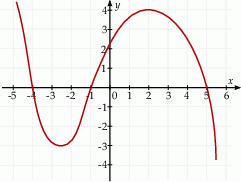
Funkcja 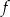 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 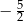 B)
B) 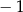 C)
C) 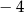 D) 2
D) 2
Kąt  jest ostry oraz
jest ostry oraz 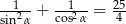 . Wartość wyrażenia
. Wartość wyrażenia 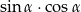 jest równa
jest równa
A)  B)
B)  C)
C) 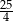 D)
D) 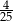
Kąt  jest rozwarty oraz
jest rozwarty oraz 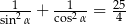 . Wartość wyrażenia
. Wartość wyrażenia 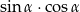 jest równa
jest równa
A) 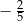 B)
B)  C)
C) 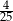 D)
D)