Ze zbioru liczb 3, 4, 1, 5, 1, 3, 1 usunięto jedną liczbę w ten sposób, że mediana tego zbioru liczb nie uległa zmianie. Usunięta liczba to
A) 1 B) 3 C) 4 D) 5
/Szkoła średnia/Zadania testowe
Równanie 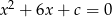 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 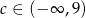 B)
B) 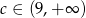 C)
C) 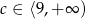 D)
D) 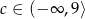
Równanie 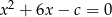 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 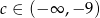 B)
B) 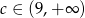 C)
C) 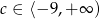 D)
D) 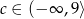
Równanie 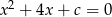 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 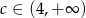 B)
B) 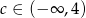 C)
C) 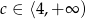 D)
D) 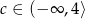
W równoległoboku 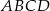 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 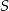 . Niech
. Niech 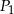 oznacza pole trójkąta
oznacza pole trójkąta 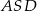 , natomiast
, natomiast 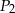 oznacza pole trójkąta
oznacza pole trójkąta 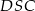 . Wówczas:
. Wówczas:
A) 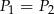 B)
B) 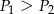 C)
C) 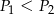 D)
D) 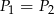 tylko wtedy, gdy
tylko wtedy, gdy 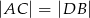
W równoległoboku 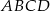 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 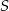 . Niech
. Niech 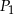 oznacza pole trójkąta
oznacza pole trójkąta 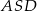 , natomiast
, natomiast 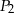 oznacza pole trójkąta
oznacza pole trójkąta 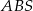 . Wówczas:
. Wówczas:
A) 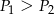 B)
B) 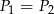 C)
C) 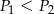 D)
D) 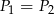 tylko wtedy, gdy
tylko wtedy, gdy 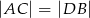
Cięciwy 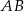 i
i 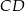 okręgu o środku
okręgu o środku 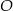 przecinają się w punkcie
przecinają się w punkcie 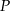 i tworzą trójkąty
i tworzą trójkąty 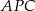 i
i 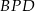 .
.
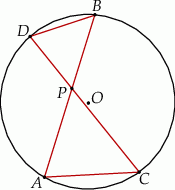
Trójkąty 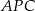 i
i 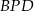 są
są
| A) podobne, | B) przystające, |
ponieważ trójkąty te mają równe
| 1) pola, | 2) miary kątów, | 3) długości boków, |
Gdy przesuniemy wykres funkcji 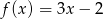 o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 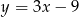 B)
B) 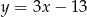 C)
C) 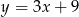 D)
D) 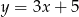
Aby otrzymać wykres funkcji 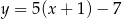 , należało wykres funkcji
, należało wykres funkcji 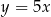 przesunąć
przesunąć
A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
C) o 1 jednostkę w prawo i 7 ku dołowi D) o 1 jednostkę w lewo i 7 ku górze
Gdy przesuniemy wykres funkcji 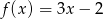 o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 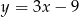 B)
B) 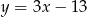 C)
C) 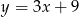 D)
D) 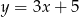
Punkty 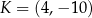 i
i 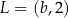 są końcami odcinka
są końcami odcinka 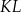 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 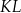 jest równa
jest równa 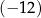 . Wynika stąd, że
. Wynika stąd, że
A) 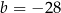 B)
B) 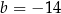 C)
C) 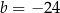 D)
D) 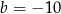
Wykres funkcji 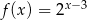 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
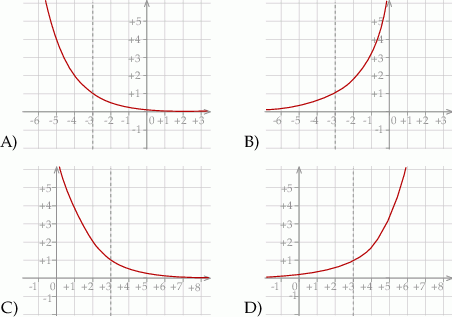
Wykres funkcji 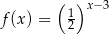 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
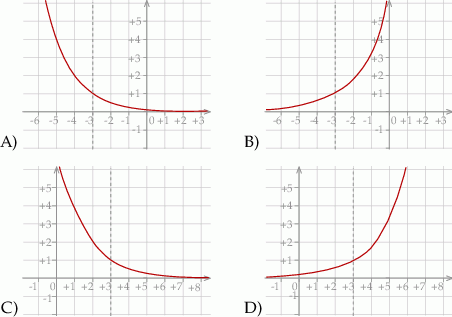
Wykres funkcji 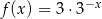 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
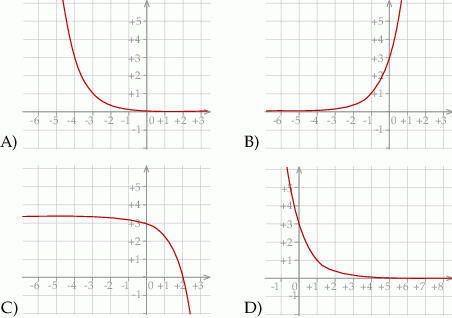
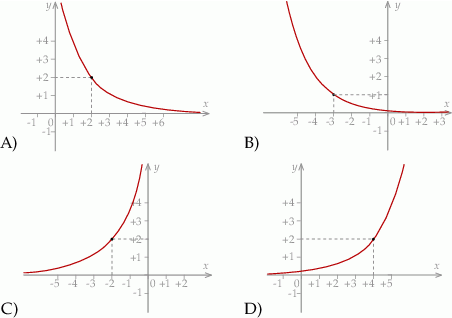
Wykres funkcji 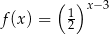 przedstawiony jest na rysunku
przedstawiony jest na rysunku
Liczba 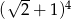 jest większa od liczby
jest większa od liczby 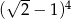 o
o
A) 2 B) 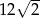 C)
C) 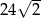 D)
D) 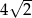
Pole powierzchni bocznej walca wynosi 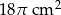 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 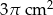 B)
B) 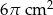 C)
C) 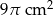 D)
D) 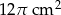
Odcinek 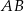 jest średnicą okręgu (rysunek).
jest średnicą okręgu (rysunek).
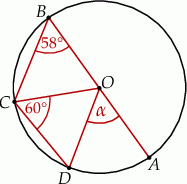
Miara kąta  jest równa
jest równa
A) 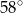 B)
B) 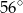 C)
C) 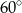 D)
D) 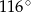
Ciąg arytmetyczny 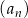 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 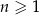 . Piąty wyraz tego ciągu jest o 12 większy od trzeciego wyrazu. Wtedy różnica
. Piąty wyraz tego ciągu jest o 12 większy od trzeciego wyrazu. Wtedy różnica 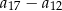 jest równa
jest równa
A) 60 B) 6 C) 30 D) 24

