Wyrażenie 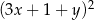 jest równe
jest równe
A) 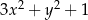 B)
B) 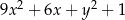
C) 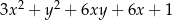 D)
D) 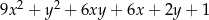
/Szkoła średnia/Zadania testowe
Wyrażenie 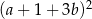 jest równe
jest równe
A) 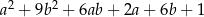 B)
B) 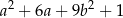
C) 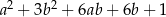 D)
D) 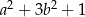
W rozwinięciu dziesiętnym ułamka 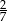 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Liczbę 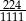 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 6
W rozwinięciu dziesiętnym ułamka 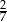 na czterdziestym miejscu po przecinku stoi cyfra
na czterdziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Liczbę 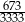 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 9
W rozwinięciu dziesiętnym ułamka 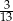 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 6 B) 9 C) 2 D) 3
W rozwinięciu dziesiętnym ułamka 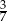 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Ciąg 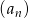 określony jest wzorem
określony jest wzorem 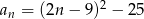 , gdzie
, gdzie 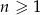 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 4 B) 5 C) 6 D) 7
Czworokąt 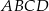 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 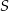 . Bok
. Bok 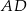 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 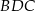 jest równa
jest równa 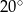 (zobacz rysunek).
(zobacz rysunek).
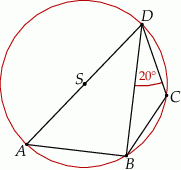
Wtedy miara kąta 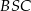 jest równa
jest równa
A) 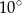 B)
B) 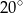 C)
C) 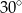 D)
D) 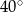
Czworokąt 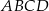 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 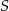 . Bok
. Bok 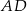 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 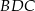 jest równa
jest równa 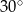 (zobacz rysunek).
(zobacz rysunek).
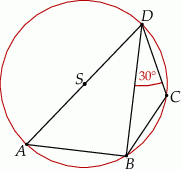
Wtedy miara kąta 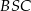 jest równa
jest równa
A) 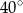 B)
B) 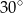 C)
C) 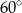 D)
D) 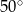
Suma kolejnych dodatnich liczb nieparzystych mniejszych od 100 jest równa
A) 2500 B) 5050 C) 2450 D) 2525
Suma wszystkich liczb całkowitych dodatnich parzystych i jednocześnie mniejszych od 1001 jest równa
A) 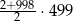 B)
B) 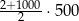 C)
C) 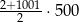 D)
D) 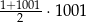
Suma kolejnych liczb dodatnich parzystych mniejszych od 100 jest równa
A) 2550 B) 4900 C) 2450 D) 2525
Suma kolejnych dodatnich liczb nieparzystych mniejszych od 200 jest równa
A) 9801 B) 10201 C) 9900 D) 10000
Suma wszystkich liczb całkowitych dodatnich nieparzystych i jednocześnie mniejszych od 1000 jest równa
A) 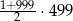 B)
B) 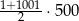 C)
C) 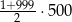 D)
D) 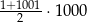
W grupie 24 osób (mężczyzn i kobiet) jest 3 razy więcej kobiet niż mężczyzn. Z grupy tej losujemy 2 osoby. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowano osoby różnej płci to
A) 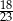 B)
B)  C)
C) 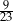 D)
D) 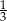
Pierwsza rata, która stanowi 9% ceny kanapy, jest o 84 zł niższa od drugiej raty, która stanowi 12% ceny kanapy. Kanapa kosztuje
A) 280 zł B) 2788 zł C) 2520 zł D) 2800 zł
Pierwsza rata, która stanowi 10% ceny aparatu, jest o 19 zł niższa od drugiej raty, która stanowi 15% ceny aparatu. Aparat kosztuje
A) 380 zł B) 38 zł C) 420 zł D) 360 zł
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 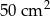 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 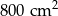 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 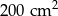 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Dziedziną wyrażenia wymiernego 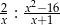 jest zbiór
jest zbiór
A) 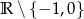 B)
B) 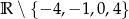 C)
C) 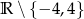 D)
D) 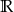
Dziedziną wyrażenia wymiernego 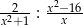 jest zbiór
jest zbiór
A) 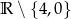 B)
B) 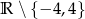 C)
C) 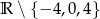 D)
D) 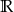
Dziedziną wyrażenia wymiernego 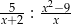 jest zbiór
jest zbiór
A) 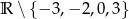 B)
B) 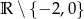 C)
C) 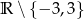 D)
D) 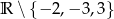
W trójkącie 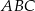 , w którym
, w którym 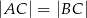 , na boku
, na boku 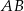 wybrano punkt
wybrano punkt 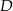 taki, że
taki, że 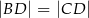 oraz
oraz 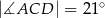 (zobacz rysunek).
(zobacz rysunek).
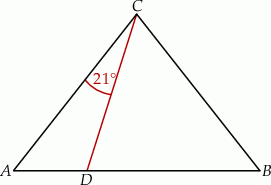
Wynika stąd, że kąt  ma miarę
ma miarę
A)  B)
B)  C)
C) 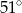 D)
D) 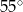
W trójkącie 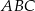 , w którym
, w którym 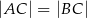 , na boku
, na boku 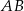 wybrano punkt
wybrano punkt 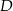 taki, że
taki, że 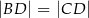 oraz
oraz 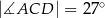 (zobacz rysunek).
(zobacz rysunek).
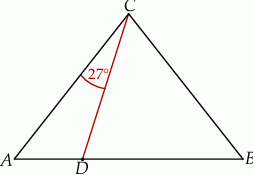
Wynika stąd, że kąt 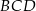 ma miarę
ma miarę
A) 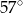 B)
B)  C)
C) 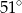 D)
D) 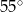
Dany jest trójkąt równoramienny 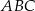 , w którym
, w którym 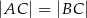 . Na podstawie
. Na podstawie 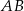 tego trójkąta leży punkt
tego trójkąta leży punkt 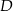 , taki że
, taki że 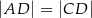 ,
, 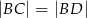 oraz
oraz 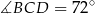 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że kąt  ma miarę
ma miarę
A)  B)
B) 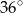 C)
C) 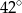 D)
D) 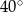
Dany jest trójkąt równoramienny 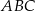 , w którym
, w którym 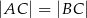 . Na podstawie
. Na podstawie 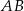 tego trójkąta leży punkt
tego trójkąta leży punkt  , taki że
, taki że 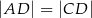 ,
, 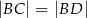 oraz
oraz 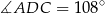 (zobacz rysunek).
(zobacz rysunek).
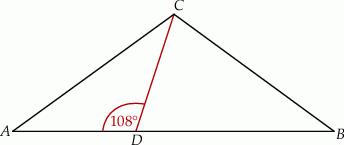
Wynika stąd, że kąt 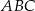 ma miarę
ma miarę
A) 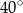 B)
B) 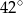 C)
C) 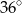 D)
D) 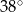
Okrąg o środku 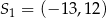 oraz okrąg o środku
oraz okrąg o środku 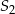 i promieniu 8 są styczne zewnętrznie w punkcie
i promieniu 8 są styczne zewnętrznie w punkcie 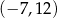 . Wtedy
. Wtedy
A) 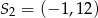 B)
B) 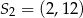 C)
C) 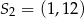 D)
D) 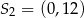
Zbiorem wartości funkcji kwadratowej 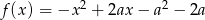 jest przedział
jest przedział 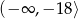 . Zatem
. Zatem
A) 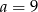 B)
B) 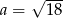 C)
C) 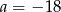 D)
D) 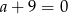
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 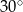 B)
B) 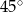 C)
C) 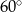 D)
D) 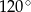
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od przekątnej podstawy tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 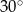 B)
B) 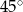 C)
C) 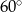 D)
D) 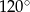
Długość przekątnej podstawy graniastosłupa prawidłowego czworokątnego jest równa długości jego wysokości. Z tego wynika, że miara kąta, jaki tworzy przekątna graniastosłupa z podstawą, jest równa
A) 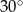 B)
B) 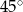 C)
C) 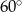 D)
D) 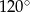
Wielomian 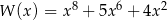 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 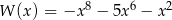 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 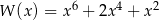 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) wartości niedodatnie B) wartości nieujemne
C) tylko wartości ujemne D) tylko wartości dodatnie
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 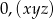 . Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 732 B) 273 C) 244 D) 723
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 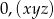 . Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka  jest więc równy
jest więc równy
A) 79 B) 273 C) 237 D) 244
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 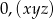 . Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 372 B) 273 C) 244 D) 124
Przekątne trapezu 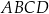 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że
w ten sposób, że 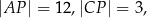
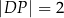 . Długość odcinka
. Długość odcinka 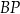 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątne trapezu 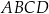 o podstawach
o podstawach 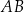 i
i 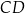 przecinają się w punkcie
przecinają się w punkcie 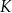 w ten sposób, że
w ten sposób, że 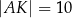 ,
, 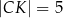 ,
, 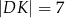 . Długość odcinka
. Długość odcinka 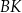 jest równa
jest równa
A) 7 B) 14 C) 10 D) 8
Przekątne trapezu 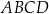 przecinają się w punkcie
przecinają się w punkcie 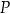 w ten sposób, że
w ten sposób, że 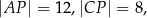
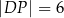 . Długość odcinka
. Długość odcinka 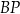 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
W ciągu arytmetycznym 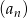 dla
dla 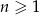 ,
, 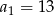 oraz
oraz 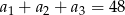 . Wtedy suma
. Wtedy suma 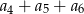 jest równa
jest równa
A) 48 B) 96 C) 75 D) 58
Przekątna równoległoboku dzieli go na dwa trójkąty równoramienne (zobacz rysunek).
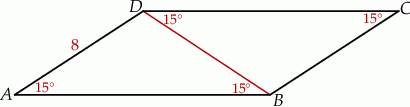
Pole tego równoległoboku jest równe
A) 16 B) 32 C) 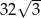 D)
D) 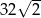
W trójkącie jeden z kątów jest o 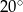 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 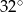 B)
B) 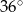 C)
C) 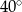 D)
D) 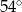
W trójkącie jeden z kątów jest o 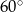 większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 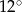 B)
B) 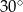 C)
C) 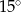 D)
D) 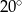
W trójkącie miary kątów są równe:  ,
, 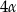 ,
, 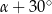 . Miara największego kąta tego trójkąta jest równa
. Miara największego kąta tego trójkąta jest równa
A) 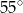 B)
B) 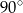 C)
C) 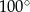 D)
D) 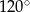
W trójkącie jeden z kątów jest o 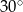 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 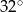 B)
B) 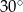 C)
C) 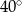 D)
D) 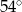
Jeden z kątów trójkąta jest trzy razy większy od drugiego. Miara trzeciego kąta jest o 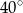 większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
A) 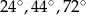 B)
B) 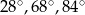 C)
C) 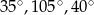 D)
D) 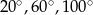
W klasie jest cztery razy więcej chłopców niż dziewcząt. Ile procent wszystkich uczniów tej klasy stanowią dziewczęta?
A) 4% B) 5% C) 20% D) 25%
W loterii fantowej jest 9 razy więcej losów przegrywających niż wygrywających. Ile procent wszystkich losów w tej loterii stanowią losy wygrywające?
A) 1% B) 11% C) 10% D) 90%

