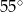W trójkącie prostokątnym miary kątów ostrych są równe  i
i 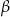 . Wartość wyrażenia
. Wartość wyrażenia 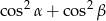 jest równa
jest równa
A) 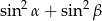 B)
B) 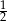 C)
C) 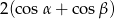 D)
D) 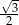
/Szkoła średnia/Zadania testowe
Punkty 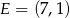 i
i 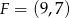 to środki boków, odpowiednio
to środki boków, odpowiednio 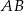 i
i 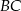 kwadratu
kwadratu 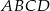 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 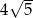 B) 10 C)
B) 10 C) 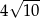 D) 20
D) 20
Punkty 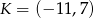 i
i 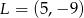 to środki boków, odpowiednio
to środki boków, odpowiednio 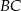 i
i 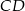 kwadratu
kwadratu 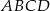 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 32 B) 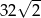 C)
C) 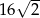 D) 16
D) 16
Dla każdej dodatniej liczby  iloraz
iloraz 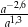 jest równy
jest równy
A) 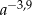 B)
B) 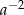 C)
C) 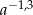 D)
D) 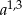
Dla każdej dodatniej liczby  iloraz
iloraz 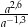 jest równy
jest równy
A) 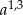 B)
B) 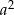 C)
C) 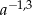 D)
D) 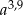
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 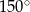 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 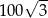 D)
D) 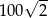
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 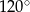 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 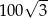 D)
D) 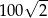
Pole powierzchni trójkąta równoramiennego o ramionach długości 6 cm i kącie między nimi 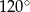 jest równe
jest równe
A) 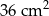 B)
B) 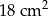 C)
C) 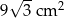 D)
D) 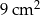
Ramię trójkąta równoramiennego 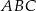 ma długość 8, a jeden z kątów tego trójkąta ma miarę
ma długość 8, a jeden z kątów tego trójkąta ma miarę 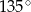 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 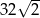 B)
B) 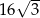 C) 32 D)
C) 32 D) 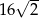
Wierzchołki trójkąta 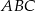 mają współrzędne
mają współrzędne 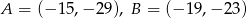 i
i 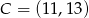 . Bok
. Bok 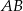 trójkąta
trójkąta 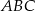 ma długość
ma długość
A) 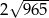 B)
B) 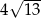 C)
C) 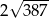 D)
D) 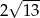
Funkcja
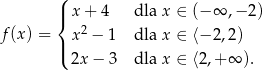
A) nie ma miejsc zerowych B) ma trzy miejsca zerowe
C) ma jedno miejsce zerowe D) ma dwa miejsca zerowe
Funkcja 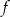 określona jest wzorem
określona jest wzorem
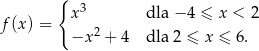
Prawdziwa jest nierówność
A) 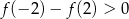 B)
B) 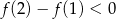
C) 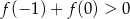 D)
D) 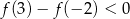
Funkcja 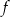 określona jest wzorem
określona jest wzorem
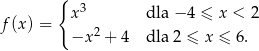
Prawdziwa jest nierówność
A) 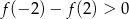 B)
B) 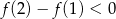
C) 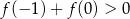 D)
D) 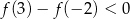
Funkcja 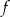 określona jest wzorem
określona jest wzorem
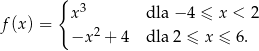
Prawdziwa jest nierówność
A) 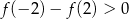 B)
B) 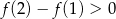
C) 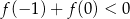 D)
D) 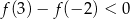
Dany jest ciąg arytmetyczny, w którym 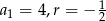 . Wtedy
. Wtedy
A) 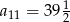 B)
B) 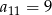 C)
C) 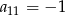 D)
D) 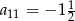
Liczba 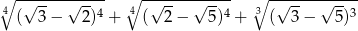 jest równa
jest równa
A) 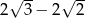 B)
B) 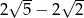 C)
C) 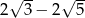 D)
D) 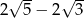
Liczba 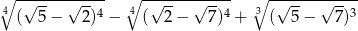 jest równa
jest równa
A) 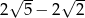 B)
B) 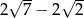 C)
C) 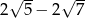 D)
D) 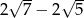
W ciągu arytmetycznym 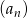 określonym dla
określonym dla 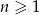 dane są
dane są 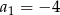 i
i 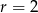 . Którym wyrazem tego ciągu jest liczba 156?
. Którym wyrazem tego ciągu jest liczba 156?
A) 81 B) 80 C) 76 D) 77
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 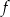 określonej wzorem
określonej wzorem 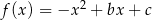 . Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne
. Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne 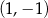 .
.
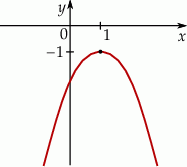
Stąd wynika, że:
A) 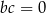 B)
B) 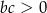 C)
C) 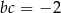 D)
D) 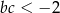
Zbiorem wartości funkcji kwadratowej 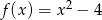 jest
jest
A) 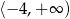 B)
B) 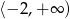 C)
C) 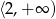 D)
D) 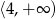
Zbiorem wartości funkcji kwadratowej 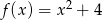 jest
jest
A) 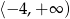 B)
B) 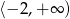 C)
C) 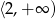 D)
D) 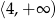
Funkcja 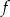 jest określona wzorem
jest określona wzorem 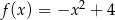 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 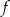 jest przedział
jest przedział
A) 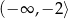 B)
B) 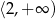 C)
C) 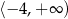 D)
D) 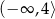
Wartość wyrażenia 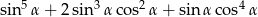 jest równa
jest równa
A) 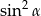 B)
B) 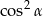 C)
C) 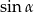 D)
D) 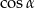
Wyrażenie 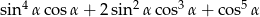 jest równe
jest równe
A) 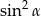 B)
B) 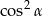 C)
C) 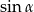 D)
D) 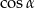
Wysokość rombu o boku długości 6 i kącie ostrym 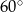 jest równa
jest równa
A) 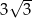 B) 3 C)
B) 3 C) 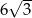 D) 6
D) 6
Wysokość rombu o boku długości 8 i kącie ostrym 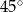 jest równa
jest równa
A) 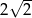 B) 4 C)
B) 4 C) 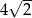 D) 8
D) 8
Do wykresu funkcji 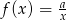 , dla
, dla 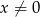 należy punkt
należy punkt 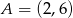 . Wtedy
. Wtedy
A) 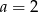 B)
B) 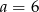 C)
C) 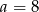 D)
D) 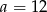
Do wykresu funkcji 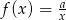 , dla
, dla 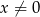 należy punkt
należy punkt 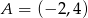 . Wtedy
. Wtedy
A) 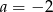 B)
B) 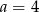 C)
C) 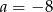 D)
D) 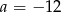
Liczba 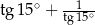 jest równa
jest równa
A) 4 B) 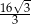 C) 1 D)
C) 1 D) 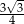
Liczba 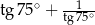 jest równa
jest równa
A) 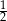 B)
B) 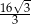 C) 4 D)
C) 4 D) 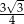
Liczba 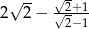 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) większą niż 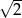 D) naturalną
D) naturalną
Liczba 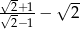 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) mniejszą niż 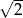 D) naturalną
D) naturalną
Dany jest sześciokąt foremny 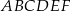 o polu równym
o polu równym 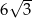 (zobacz rysunek).
(zobacz rysunek).
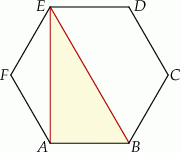
Pole trójkąta 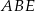 jest równe
jest równe
A) 6 B) 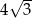 C)
C) 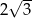 D) 4
D) 4
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 9 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) osiemnastokąt. D) dziesięciokąt.
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 10 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) jedenastokąt. D) dziesięciokąt.
Na trójkącie 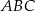 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 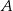 (zobacz rysunek obok).
(zobacz rysunek obok).
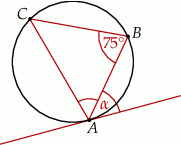
Jeżeli 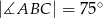 i kąt dopisany
i kąt dopisany  jest równy
jest równy 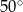 , to kąt
, to kąt 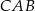 ma miarę:
ma miarę:
A) 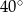 B)
B) 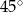 C)
C) 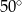 D)
D)